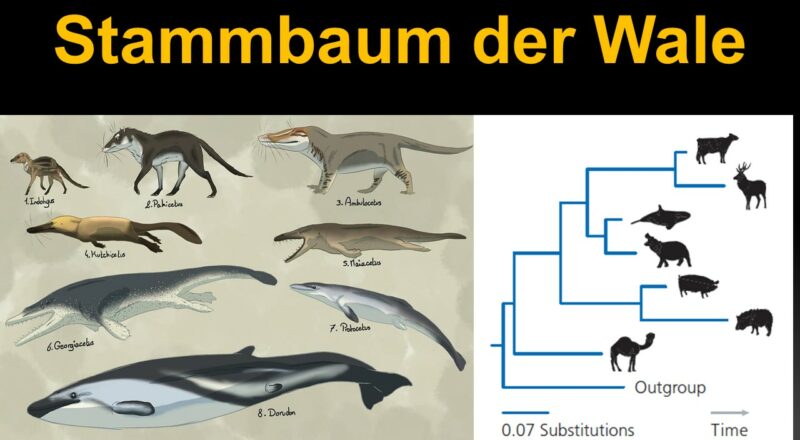
Ein evolutionärer Stammbaum stellt die verwandtschaftlichen Beziehungen einer Gruppe von Organismen dar, wie sie nach Darwins Theorie der Abstammung mit Modifikation von gemeinsamen Vorfahren verstanden werden.

In unserem letzten Tutorial hatten wir das Prinzip der Maximum Parsimonie kennengelernt und am Beispiel von drei fiktiven Antilopenarten mittels Parsimonieverfahren ein Kladogramm erstellt. Dieses Mal gehen wir einen Schritt weiter und lernen weitere Methoden der Stammbaumrekonstruktion kennen und üben dies anhand eines realen Beispiels: der Evolution der Wale

Apomorphien der Wale

Text als pdf

Die Wale (Cetacea) sind als monophyletische Gruppe durch eine Reihe von Synapomorphien des Schädels gekennzeichnet (Uhen 2007, 2010). Sie haben einen vergrößerten und verdickten Gehörgang, eine knöcherne Schale an der Schädelbasis, die die Strukturen des Ohrs umgibt. Es wird angenommen, dass dies eine Anpassung an das Hören unter Wasser ist (Nummela et al. 2007). Wale haben einen Schädel mit einer schmalen postorbitalen/temporalen Region. Außerdem haben sie eine verlängerte Schnauze, bei der die Schneide- und Eckzähne in einer Linie mit den Backenzähnen stehen und nicht wie bei den meisten Säugetieren in einem Bogen über die Vorderseite des Mundes. Diese drei evolutionären Neuerungen werden durch die Anatomie des Fossils Durodon atrox veranschaulicht, die in Abb. 1 dargestellt ist.

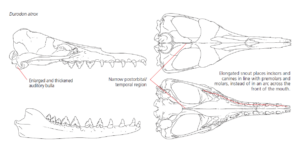
Abb. 1: Der Schädel von Durodon atrox. Dieses 37 Millionen Jahre alte Fossil veranschaulicht drei der gemeinsamen abgeleiteten Merkmale, die die Klade der Cetacea definieren, zu deren lebenden Mitgliedern die Wale gehören. Aus Uhen (2010).

Es mag seltsam erscheinen, dass wir Merkmale wie das Fehlen von Beinen und das Vorhandensein von Brustflossen nicht erwähnt haben. Dies sind schließlich die offensichtlichsten Merkmale, die Wale haben, um sich an das Leben im Wasser anzupassen. Aber die frühesten Wale hatten diese Merkmale nicht. Durodon zum Beispiel hatte Hinterbeine – wenn auch kleine. Die frühesten Wale, die aus etwa 53 Millionen Jahre alten Gesteinsschichten im Himalaya stammen, hatten ausgewachsene Hinterbeine und verbrachten wahrscheinlich einen Teil ihrer Zeit an Land (Thewissen & Hussain 1993; Thewissen et al. 1994; Bajpai & Gingerich 1998). Die fossilen Belege deuten also darauf hin, dass die modernen Wale von terrestrischen Vorfahren abstammen. Aber wer waren diese Vorfahren? Und welche der heutigen Landsäugetiere sind die nächsten lebenden Verwandten der modernen Wale?

 

Morphologische Beweise für den Ursprung der Cetacea

 

Bereits 1883 spekulierte William H. Flower (Flower 1883) aufgrund gemeinsamer Merkmale verschiedener innerer Organe darüber, dass die Wale mit den Huftieren verwandt sein könnten. Mit einer gewissen Laune erwähnte Flower Schweine als mögliche nächste lebende Verwandte der Wale. Damit würden die Wale zu den Paarhufern gehören, den Säugetieren mit einer geraden Anzahl an Zehen, zu deren lebenden Vertretern Rinder, Hirsche, Schafe, Flusspferde, Schweine, Pekaris und Kamele gehören. 1966 argumentierte Leigh Van Valen (Van Valen 1966) auf der Grundlage gemeinsamer Zahnmerkmale in Fossilien, dass Wale von einer alten Huftiergruppe, den Mesonychia, abstammen. Damit wären die Wale zwar mit den Paarhufern verwandt, gehörten aber nicht zu diesen. In Abb. 2 werden die beiden Hypothesen miteinander verglichen.

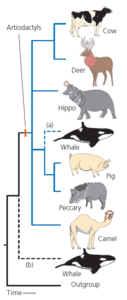
Abb. 2: Zwei Hypothesen über den Ursprung der Wale: (a) Wale sind Paarhufer; (b) Wale sind mit den Paarhufern verwandt.

Unter der Anwendung der Parsimonie-Verfahren scheinen Untersuchungen morphologischer Merkmale die Hypothese zu stützen, dass Wale zwar mit Paarhufern verwandt sind, aber nicht zu diesen gehören (O’Leary & Geisler 1999). Eine vereinfachte Version dieses Stammbaums ist in Abb. 3 dargestellt. Dieses Ergebnis war aber nicht ganz zufriedenstellend.

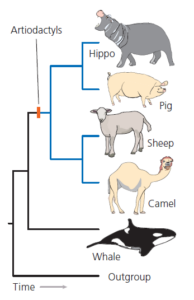
Abb. 3: Ein Baum, der nahelegt, dass Wale und Delfine mit den Paarhufern verwandt sind. Vereinfacht dargestellt nach O’Leary & Geisler (1999).

Die auffälligste Synapomorphie, die die Paarhufer als monophyletische Gruppe ausweist, ist die Form eines Knochens im Knöchel, des Astragalus (Luckett & Hong 1998; Thewissen et al. 1998). Die einzigartige Form des Astragalus der Paarhufer ist in Abb. 4 dargestellt.

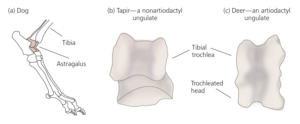
Abb. 4: Der Astragalus ist eine Synapomorphie, die die Paarhufer (Artiodatyla) kennzeichnet. (a) Der Astragalus ist der oberste Knochen des Knöchels, um den sich der Fuß dreht, um vorwärts oder rückwärts zu strecken. (b) Der Astragalus eines nicht Nicht-Paarhufers (links) und eines Paarhufers (rechts). Bei Paarhufern sind beide Enden des Astragalus rollenförmig. Nach Schaeffer (1948) und Gingerich (2001).

Bei den meisten Säugetieren ist der Kopf des Astragalus abgerundet und bildet die Kugel in einem Kugelgelenk mit den weiter zum Fuß hin gelegenen Knochen (dem Strahlbein und manchmal dem Würfelbein). Bei den Paarhufern ist der Kopf des Astragalus stattdessen scheibenförmig und bildet ein Scharniergelenk – auch Trochlea genannt (Thewissen & Madar 1999). Diese Form ermöglicht es dem Fuß sich in einem weiten Bogen um das Ende des Knöchels zu drehen und trägt zu den langen Schritten und der starken Lauffähigkeit bei, die bei vielen Paarhufern zu beobachten sind. Lebende Wale haben natürlich keine Fußgelenke. Die Form ihres Astragalus kann nicht beurteilt werden. Wie wir bereits festgestellt haben, haben einige fossile Wale Hinterbeine. Bei einigen dieser ausgestorbenen Arten, wie z. B. Basilosaurus, sind die Beine jedoch winzig und der Astragalus ist mit anderen Knochen im Knöchelbereich verschmolzen, so dass es unmöglich ist, seine Form zu beurteilen (Gingerich et al. 1990). In anderen Fällen waren die bekannten Exemplare bis vor kurzem zu fragmentarisch, um endgültige Schlüsse darüber zu ziehen, ob die Knöchel der Wale diese als Paarhufer qualifizieren (Thewissen et al. 1998; Thewissen & Madar 1999). Angesichts dieser Ungewissheit war es sinnvoll, andere Arten von Daten heranzuziehen.

 

Molekulare Beweise für die evolutionäre Verwandtschaft

 

DNA-Sequenzen und andere molekulare Merkmale bieten eine zusätzliche Informationsquelle, die wir nutzen können, um evolutionäre Beziehungen abzuschätzen. Im Vergleich zu morphologischen Merkmalen haben molekulare Merkmale sowohl Nachteile als auch Vorteile. Nachteilig ist, dass DNA- oder Proteinsequenzen zwar manchmal aus Fossilien gewonnen werden können (Campbell et al. 2010; Green et al. 2010; Lari et al. 2011), molekulare Daten jedoch nur für kürzlich ausgestorbene Taxa zur Verfügung stehen. Und da an jeder Stelle einer DNA-Sequenz nur vier Merkmalsausprägungen existieren (A, C, G und T), kann Homoplasie schwer zu erkennen und fast unmöglich vollständig zu vermeiden sein. Positiv zu vermerken ist, dass dank des technologischen Fortschritts die Kosten für die Erzeugung großer Mengen von Sequenzdaten drastisch gesunken sind. Darüber hinaus haben Evolutionsbiologen ausgefeilte Modelle entwickelt, um zu analysieren, wie sich verschiedene Arten von DNA-Sequenzen im Laufe der Zeit verändern sollten. Bei richtiger Anwendung ermöglichen diese Modelle eine genaue Schätzung der durch die Daten implizierten Phylogenie. Im Folgenden werden die Methoden zur Ableitung von Phylogenien aus DNA-Sequenzen anhand von Beispielen von Paarhufern und Walen kurz erläutert. Unsere Diskussion ist als Überblick gedacht. Für praktische Anleitungen siehe Baldauf (2003), Harrison & Langdale (2006) und Hall (2011). Für detailliertere theoretische Abhandlungen siehe Graur & Li (2000) und Felsenstein (2004).

Abgleich von Sequenzen (Alignment)

 

Um molekulare Sequenzen miteinander zu vergleichen, nimmt man z. B. ein Gen aus verschiedenen Abstammungslinien, die von einer gemeinsamen Vorfahrenkopie abstammen. Wichtig hierbei ist, dass die Sequenzen ausgerichtet sind. Man spricht hier vom Alignment. In der Bioinformatik ist ein Alignment eine Möglichkeit, die Sequenzen von DNA, RNA oder Protein anzuordnen, um Regionen mit Ähnlichkeit zu identifizieren, die eine Folge evolutionärer Beziehungen zwischen den Sequenzen sein können.

Ausgerichtete Sequenzen werden typischerweise als Zeilen innerhalb einer Matrix dargestellt. Bei einem Vergleich von zwei oder mehr Sequenzen werden diese so ausgerichtet, dass sie in möglichst vielen Positionen identisch oder ähnlich besetzt sind.

Das bedeutet, dass z. B. alle Insertionen (also Einbau zusätzlicher Nukleotide) oder Deletionen (also Verlust von Nukleotiden), die in einigen Abstammungslinien aufgetreten sind, in anderen aber nicht, identifiziert wurden und die Sequenzen verschoben wurden, um sie in Übereinstimmung zu bringen (Abb. 5).

Abb. 5: Darstellung eines Alignments

 

Sequenzen mit hoher Ähnlichkeit oder gar Identität stammen mit entsprechend hoher Wahrscheinlichkeit von einer gemeinsamen Vorläufersequenz ab, sind also homolog.

Um ein fehlerhaftes manuelles Alignment zu vermeiden oder zu reduzieren, bedient man sich diverser effizienter Programme, z. B. FASTA und BLAST. Die Qualität der Stammbaumrekonstruktion hängt wesentlich vom richtigen Alignment ab. Das heißt, die Basenpositionen der zu vergleichenden Sequenzen sollten möglichst fehlerfrei bestimmt werden (siehe Liu et al. 2009). Die korrekte Ausrichtung ist entscheidend. Wenn Sequenzen schlecht ausgerichtet sind, können die darin enthaltenen Informationen über die Evolutionsgeschichte verloren gehen (vgl. Wong et al. 2008, Ogden & Rosenberg 2006; Wang et al. 2011).

In unserem Beispiel werden Sequenzen aus dem Exon 7 des Gens für ein Milchprotein namens β-Casein (Gatesy et al. 1999) verwendet. Neben anderen Insertionen und Deletionen weist die Kuhsequenz im Vergleich zur Walsequenz eine 3-Nukleotid lange Deletion auf, die an Stelle 61 beginnt. Abb. 6 zeigt die Sequenzen der beiden Tiere in der Nähe der Deletion vor und nach dem Alignment.

Abb. 6: Sequenzen vor und nach dem Alignment. Vergleichen Sie diese kurzen Abschnitte des Gens für β-Casein, und die Aminosäuren die es kodiert, vor und nach dem Alignment

Zur Veranschaulichung der verschiedenen Methoden zur Ableitung von Phylogenien verwenden wir die in Abbildung 7 gezeigten acht alignierten Sequenzen. Diese sind ein kleiner Teil des β-Casein-Gens und stellen einen Bruchteil eines viel größeren Datensatzes dar, der von John Gatesy et al. (1999) analysiert wurde.

Abb. 7: Sequenzdaten für die Inferenz der Phylogenie. Diese Tabelle zeigt 60 Nukleotide der alignierten Sequenz (Stellen 141 bis 200) von Exon 7 des β-Casein-Gens. Die Daten stammen von sechs Paarhufern, einem Wal (dem Delphin Lagenorhynchus obscurus) und einem Rhinozeros als Außengruppe (Gatesy et al. 1999). Ein X an einer Stelle steht für ein nicht eindeutig identifiziertes Nukleotid.

Bewertung alternativer Phylogenien mit Parsimonie

 

Eine Möglichkeit zur Schätzung von Evolutionsbäumen anhand von Sequenzdaten besteht darin, jede Stelle in der Sequenz als unabhängiges Merkmal zu behandeln und nach Synapomorphien zu suchen, die monophyletische Gruppen identifizieren. Das heißt, wir können die Nukleotide an den Sequenzstellen auf die gleiche Weise analysieren, wie wir die morphologischen Merkmale im letzten Tutorial analysiert haben. Die Untersuchung der Sequenzen in Abbildung 7 zeigt, dass einige Stellen uninformativ sind. An Position 142 zum Beispiel haben alle acht Taxa denselben Merkmalsstatus, ein G. An Position 192 unterscheidet sich nur ein Taxon, Kamele, von den anderen sieben.

Andere Bereiche sind informativ. Position 166 weist ein offenbar gemeinsames abgeleitetes Merkmal, ein C, auf, das Wale und Nilpferde als Schwesterlinien ausweist. Und diese Synapomorphie ist in eine andere eingebettet, ein T an Position 162, das Kühe, Hirsche, Wale und Flusspferde als monophyletische Gruppe zu identifizieren scheint. Die Merkmale an Position 162 stehen jedoch im Widerspruch zu denen an Position 177. Dort scheint T ein gemeinsames abgeleitetes Merkmal zu sein, das Wale, Flusspferde, Schweine und Pekaris als eine monophyletische Gruppe identifiziert. Wir haben es hier eindeutig mit einem nicht idealen Fall zu tun. Als wir auf Konflikte zwischen morphologischen Merkmalen stießen, wandten wir uns der Parsimony-Analyse zu. Das Gleiche können wir mit Sequenzdaten machen (Felsenstein 1988). Wir betrachten alle möglichen Bäume als Hypothesen, bestimmen das Minimum an Evolution, das erforderlich ist, um die Verteilung der Nukleotide an jeder Stelle in jedem Baum zu erklären, und suchen den Baum, der insgesamt die geringste Veränderung erfordert.

In Abb. 8 werden zwei mögliche Bäume (von 10.395) gezeigt, die drei der 60 Molekularen Merkmale zeigen, nämlich die Nukleotide an den Positionen 162, 166 und 177. Baum (a), in dem die Wale zu den Paarhufern gehören und eine monophyletische Gruppe mit den Flusspferden bilden, erfordert sechs Nukleotidsubstitutionen. Baum (b), in dem die Wale lediglich mit den Paarhufern verwandt sind, aber nicht selbst zu ihnen gehören, erfordert neun. Wenn wir ein Computerprogramm (Felsenstein 2009) verwenden, um den einfachsten aller 10.395 Bäume für alle 60 Merkmale zu finden, erfahren wir, dass Baum (a) in Abb. 8 der Gewinner ist, da er 41 Substitutionen erfordert. Baum (b) 47.

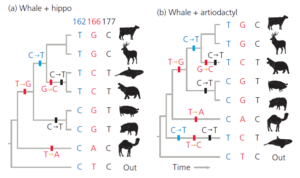
Abb. 8: Parsimony-Analyse von drei molekularen Merkmalen auf zwei Bäumen. Baum (a) erfordert sechs evolutionäre Veränderungen, während für Baum (b) neun erforderlich sind. Für diese Merkmale ist Baum (a) aussagekräftiger, weil sparsamer.

Bewertung alternativer Phylogenien mit Maximum Likelihood.

Parsimonie ist aber nicht das einzige Kriterium, das wir verwenden können, um mögliche Bäume zu bewerten und diejenigen zu identifizieren, die die beste Schätzung der evolutionären Beziehungen bieten. Eine weitere häufig verwendete Methode ist die Maximum Likelihood (Felsenstein 1981). Die Berechnungen, die mit einer Likelihood-Analyse verbunden sind, sind umständlich, aber die Grundidee ist einfach. Unsere Erklärung dieses Konzepts wird sinnvoller, wenn wir uns zunächst die Art des Baums ansehen, den wir damit erstellen können. Abb. 9 zeigt einen Baum, der mit Hilfe von Likelihood und den Daten des untersuchten β-Casein-Gens (in Abb. 7) geschätzt wurde. Dieser Baum unterscheidet sich vom Parsimonie-Baum dahingehend, dass er nicht nur Informationen über die Reihenfolge der Verzweigungen, sondern auch über die Länge der Zweige Auskunft gibt.

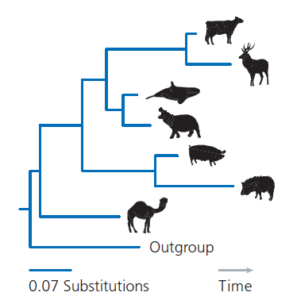
Abb. 9: Eine Maximum-Likelihood-Phylogenie. Geschätzt mit PhyML, wobei alle Optionen auf den Standardeinstellungen waren (Chevenet et al. 2006; Dereeper et al. 2008; Guindon et al. 2010).

Diese sind proportional zur Anzahl der Nukleotidsubstitutionen, die auf jedem Zweig stattgefunden haben dürften. Es wird beispielsweise angenommen, dass das Pekari mehr Substitutionen angehäuft hat als das Schwein, seit sich die beiden Linien getrennt haben. Die Schätzung der Zweiglängen ist ein wesentlicher Bestandteil einer Likelihood-Analyse. Die Wahrscheinlichkeit der Daten bei einem Baum, seinen Zweiglängen und einem Evolutionsmodell wird als Wahrscheinlichkeit des Baums bezeichnet.

Sie kann geschrieben werden als L(tree) = P(data|tree, branch lengths, model).

Es wird nicht überraschen, dass Biologen die Berechnungen fast immer mit dem Computer durchführen. Um die Evolutionsgeschichte mit Hilfe der Wahrscheinlichkeitsrechnung zu rekonstruieren, lassen Biologen eine Software laufen, die die Zweiglängen jedes möglichen Baumes so anpasst, dass die Wahrscheinlichkeit des Baumes maximiert wird, und dann die Bäume vergleicht, um denjenigen zu finden, dessen Wahrscheinlichkeit am höchsten ist (Huelsenbeck & Crandall 1997). Der Gewinner ist die Maximum-Likelihood-Schätzung der Phylogenie. Es ist der Baum mit der besten Chance, die Daten zu erzeugen. Abb. 10 zeigt ein einfaches Beispiel. Es verwendet die Daten für den Wal, das Flusspferd, das Schwein und die Außengruppe unseres Datensatzes. Mit nur drei Arten in der Ingroup gibt es drei mögliche evolutionäre Bäume. Nachdem die Zweiglängen für jeden Baum optimiert wurden, stellt man fest, dass der letzte Baum die höchste Wahrscheinlichkeit aufweist. Er deutet darauf hin, dass Wale und Flusspferde enger miteinander verwandt sind als beide mit Schweinen, und stimmt mit den vorher gezeigten Phylogenien für alle acht Taxa überein.

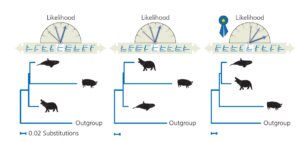
Abb. 10: Die Suche nach dem Baum mit der höchsten Wahrscheinlichkeit. Bevor die Bäume verglichen werden, die Zweiglängen der einzelnen angepasst, um die Likelihood zu maximieren.

Suche nach dem besten aller möglichen Stammbäume

 

Das Verfahren zur Schätzung einer Phylogenie durch Likelihood beginnt mit der Annahme, dass alle möglichen Bäume legitime Hypothesen sind. Die einzige Möglichkeit, sicher zu sein, den besten Baum zu finden, besteht darin, alle zu überprüfen. Bei einer großen Anzahl von Arten ist die Überprüfung aller möglichen Bäume jedoch unpraktisch. Der Grund dafür ist, dass die Anzahl der möglichen Bäume mit der Anzahl der Taxa in der Ingroup schnell ansteigt. Bei sieben Arten in der Ingroup, wie wir sie in unseren Daten haben, gibt es 10.395 mögliche Bäume. Bei 20 Arten sind es 8.200.794.532.637.891.559.375 (=Über 8 Trilliarden!). Biologen wollen in der Regel Phylogenien für eine viel größere Anzahl von Taxa als diese schätzen. Selbst mit den schnellsten Computern können wir nicht alle möglichen Bäume überprüfen. Das Problem ist in etwa so, als würde man versuchen, mit verbundenen Augen den höchsten Punkt eines Nationalparks zu finden. Im Prinzip könnten wir ein enges Raster durch den gesamten Park ziehen. Nachdem wir jeden Quadratmeter besucht hätten, wüssten wir mit Sicherheit, welcher Punkt der höchste ist. Aber wenn der Park groß ist, würde eine erschöpfende Suche viel Zeit in Anspruch nehmen. Eine Möglichkeit, unsere Suche zu beschleunigen, besteht darin, auf Hinweise zu achten, die ganze Regionen des Parks ausschließen. So müssen wir zum Beispiel nicht unter Wasser suchen. Eine andere Möglichkeit besteht darin, immer nach oben zu gehen. Dieser Plan hat den Nachteil, dass wir auf einem Hügel festsitzen könnten, ohne zu wissen, dass es anderswo im Park höhere Gipfel gibt. Dies ließe sich jedoch umgehen, indem man mehrere Suchen durchführt, die jeweils an einem anderen Ort beginnen. Die Autoren von Phylogenie-Inferenz-Software verwenden analoge Strategien, um die Suche nach dem besten aller möglichen Bäume zu beschleunigen (Felsenstein 2004). Eine dieser Strategien, Branch and Bound genannt, schließt Gruppen von Bäumen aus, wenn sich herausstellt, dass alle ihre Mitglieder schlechter sind als der beste bisher gefundene Baum. Andere Strategien, die zusammenfassend als heuristische Suche bezeichnet werden, suchen nach Bäumen, die dem aktuell führenden Baum überlegen sind, indem sie den führenden Baum auf verschiedene Weise neu anordnen und die Ergebnisse auswerten. Um zu vermeiden, dass die Suche auf einem lokalen Höhepunkt stecken bleibt, kann sie von verschiedenen Ausgangspunkten aus wiederholt werden. Oder die Suche kann mit einem Baum begonnen werden, von dem wir Grund zu der Annahme haben, dass er bereits nahe am bestmöglichen Baum ist, weil er mit einem Algorithmus erstellt wurde, der in der Regel recht gut funktioniert (Guindon & Gascuel 2003). Zu diesen Methoden gehören sog. Distanz-Matrix-Methoden wie das Neighbor-Joining (Swofford et al. 1996, Saitou & Nei 1987, Abb. 11).

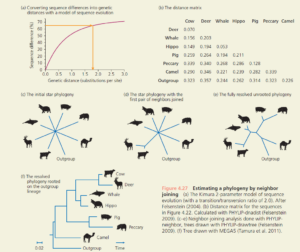
Abb. 11: Schätzung einer Phylogenie durch Neighbor-Joining-Verfahren. (a) Das 2-Parameter-Modell von Kimura für die Sequenzevolution (mit einem Verhältnis von Übergang/Umwandlung von 2,0). Nach Felsenstein (2004). (b) Distanzmatrix für die Sequenzen in Abbildung 7. Berechnet mit PHYLIP-dnadist (Felsenstein 2009). (c-e) Mit PHYLIPneighbor durchgeführte Neighbor-Joining-Analyse, Bäume gezeichnet mit PHYLIP-drawtree (Felsenstein 2009). (f) Baum gezeichnet mit MEGA5 (Tamura et al. 2011).

Wichtig ist hier zu verstehen, dass mit dieser Methode die mittlere Anzahl von Veränderungen an einer Position ermittelt wird, die zwischen einer Sequenz und ihrem Vorläufer oder zwischen 2 Sequenzen aus benachbarten Gruppierungen seit ihrem Divergieren aufgetreten sind. Die Abstände im Sequenzstammbaum werden entsprechend korrigiert. Dies setzt allerdings die Annahme voraus, dass die Zahl an Mutationen in dem vom Sequenzstammbaum erfassten Zeitraum konstant ist.

Neighbor Joining ist nicht die genaueste Methode zur Ableitung der Phylogenie, aber sie ist recht gut (Guindon & Gascuel 2003). Sie hat den großen Vorteil, dass sie auch bei großen Datensätzen schnell ist.

 

Schätzung der Unsicherheit in Phylogenien durch Bootstrapping

 

Sobald wir eine Phylogenie geschätzt haben, sollten wir uns als erstes fragen, wie viel Vertrauen wir in sie setzen können. Hängt unsere Schlussfolgerung, dass es sich bei den Walen um Paarhufer handelt, beispielsweise nur von einigen wenigen Merkmalen in unserem Datensatz ab, die wir mit viel Glück erfasst haben, oder wird sie von den meisten Merkmalen gestützt? Der beste Weg, dies herauszufinden, wäre, Daten für weitere Merkmale zu sammeln und die Analyse zu wiederholen. Und noch einmal. Wenn wir die Studie 100-mal wiederholen und feststellen würden, dass 97 unserer geschätzten Bäume die Wale den Paarhufern zuordnen, könnten wir unseren Schlussfolgerungen etwas mehr Vertrauen schenken. Aber das würde Zeit und Geld kosten, die wir vielleicht nicht haben. Eine schnelle und billige Alternative ist die Verwendung eines Computers, um die Wiederholung der Studie zu simulieren. Eine solche Methode, die häufig bei anderen statistischen Analysen eingesetzt wird, heißt Bootstrapping (Felsenstein 1985). In Abb. 12 wird seine Anwendung in einer Parsimonie-Analyse gezeigt.

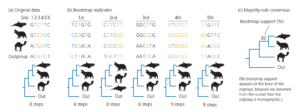
Abb. 12: Bootstrapping einer Phylogenie-Schätzung. Nach Baldauf (2003).

Abb. 12a zeigt einen imaginären Datensatz für einen Wal, ein Nilpferd, ein Kamel und eine Outgroup. Für jedes Tier haben wir eine Sequenz von sechs Nukleotiden. Die simpelste Phylogenie für unsere Ingroup zeigt den Wal und das Nilpferd als Schwestertaxa. Um diese Phylogenie mit einem Bootstrap zu überprüfen, verwenden wir unseren Computer, um aus unserem ursprünglichen Datensatz (Abb. 12b) künstliche Datensätze, so genannte Bootstrap-Wiederholungen, zu erstellen. Dazu ziehen wir eine Zufallsstichprobe mit Ersetzung aus unseren ursprünglichen Zeichen – den sechs Standorten, die jeweils in einer anderen Farbe dargestellt sind. Beachtet, dass in unserer ersten Wiederholung die Stelle 1 (schwarz) zweimal ausgewählt wurde, während die Stelle 3 (orange) ganz weggelassen wurde.

Bei der zweiten Wiederholung wurden die Standorte 4 (oliv) und 6 (dunkelblau) zweimal ausgewählt, während die Standorte 1 (schwarz) und 5 (hellblau) ausgelassen wurden. Anschließend schätzen wir die Phylogenie anhand der einzelnen Bootstrap-Wiederholungen mit der gleichen Methode, die wir für die Originaldaten verwendet haben. Für unsere 1., 3., 4. und 5. Wiederholung weist der einfachste Baum den Wal und das Nilpferd als engste Verwandte aus. Für die zweite Wiederholung hat der einfachste Baum das Kamel und das Nilpferd als Schwesterarten. Schließlich zeichnen wir einen Baum, die sogenannte Konsens-Phylogenie nach der Mehrheitsregel, die alle monophyletischen Gruppen enthält, die in mindestens der Hälfte unserer Bootstrap-Wiederholungen vorkommen (Abb. 12c). Die einzige Gruppe innerhalb unserer Ingroup, die dieses Kriterium erfüllt, ist diejenige mit dem Wal und dem Flusspferd als Schwestertaxa. Wir kennzeichnen den Knoten an der Basis dieser Klade mit dem Prozentsatz der Wiederholungen, in denen er vorkommt. Diese Zahl, die Bootstrap-Unterstützung, zeigt an, dass die Klade in unserem gesamten Datensatz ein starker Gewinner ist (Baldauf 2003). Wenn Forscher Bootstrap-Evolutionsbäume erstellen, werden in der Regel 100 oder mehr Wiederholungen erzeugt. Abb.13 zeigt die Bootstrap-Unterstützung auf der Grundlage von 1.000 Wiederholungen für mehrere monophyletische Gruppen in einer Maximum-Likelihood-Phylogenie, die aus β-Casein-Sequenzen mit 1.100 Nukleotiden Länge geschätzt wurde. In diesem Datensatz gibt es ein starkes Signal (99 % Bootstrap-Unterstützung), das darauf hinweist, dass Wale zu einer monophyletischen Gruppe mit Kühen, Hirschen, Flusspferden, Schweinen und Pekaris gehören – eingebettet in die Gattung der Paarhufer. Es gibt auch eine starke Unterstützung (100%), die darauf hinweist, dass Wale Mitglieder einer exklusiveren Klade mit Kühen, Hirschen und Flusspferden angehören. Schwächere Unterstützung gibt es (59 %) für die Hypothese, dass Wale und Nilpferde Schwestertaxa sind. Wie sehr diese Schätzung der tatsächlichen Evolutionsgeschichte der acht Arten entspricht, hängt davon ab, wie gut das β-casein-Gen den Rest des Genoms repräsentiert.

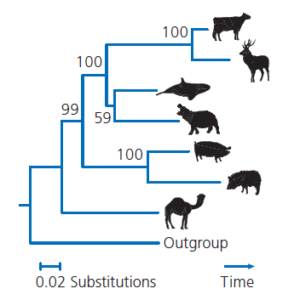
Abb. 13: Prozentsatz der Bootstrap-Unterstützung für eine Maximum-Likelihood-Phylogenie. Baum geschätzt aus 1.100 Nukleotid langen Sequenzen aus dem β-Casein-Gen (Gatesy et al. 1999). Bootstrap-Analyse mit PhyML, alle Optionen auf Standard (Guindon & Gascuel 2003).

Bayessche Phylogenie-Inferenz

Was wir wissen wollen ist aber die Wahrscheinlichkeit des Baums in Abhängigkeit von den Daten, auch bekannt als die posteriore Wahrscheinlichkeit des Baums. Hierzu bedient man sich der Bayesschen Phylogenie-Intferenz.

Diese kombiniert die Informationen in der vorherigen und in der Datenwahrscheinlichkeit, um die sogenannte posteriore, also hintere Wahrscheinlichkeit von Baumen zu erzeugen, die die Wahrscheinlichkeit ist, dass der Baum angesichts der Daten und des Wahrscheinlichkeitsmodells korrekt ist. Die Bayes’sche Inferenz wurde in den 1990er Jahren von drei unabhangigen Gruppen in die molekulare Phylogenetik eingefuhrt: Bruce Rannala und Ziheng Yang in Berkeley, Bob Mau in Madison und Shuying Li an der Universitat von Iowa, wobei die letzten beiden zu dieser Zeit Doktoranden waren (Rannala & Ziheng 1996, Yang & Rannala 1997, Mau et al. 1999, Li et al 2000). Der Ansatz ist seit der Veroffentlichung der MrBayes-Software im Jahr 2001 sehr popular geworden und ist heute eine der beliebtesten Methoden in der molekularen Phylogenetik (Huelsenbeck & Ronquist 2001).

Die Bayes’sche Inferenz bezieht sich auf eine Wahrscheinlichkeits-Methode, die von Reverend Thomas Bayes basierend auf dem Bayes’schen Theorem entwickelt wurde. wir nutzen hierfür folgende Formel (Bayes 1763, Abb. 14):

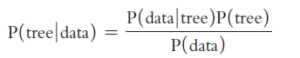
Abb. 14: Formel nach Bayes

 

Der erste Term im Zähler, P(data|tree) auf der rechten Seite ist die Wahrscheinlichkeit des Baumes. Der zweite Term, P(tree), ist die Vorwahrscheinlichkeit des Baumes. Es ist die Wahrscheinlichkeit, die wir dem Baum zugewiesen haben, bevor wir die Daten berücksichtigt haben. Der Nenner, P(data), ist die Vorwahrscheinlichkeit der Daten. Er ist die Summe der Werte, die wir durch Multiplikation der Wahrscheinlichkeit jedes möglichen Baumes mit seiner vorherigen Wahrscheinlichkeit erhalten (Huelsenbeck et al. 2001). Wir können also nur dann das berechnen, was wir wollen – die Wahrscheinlichkeit des Baumes angesichts der Daten -, wenn wir bereit sind, vorherige Wahrscheinlichkeiten für alle möglichen Bäume anzugeben (Felsenstein 2004).

Der Bayessche Ansatz zur phylogenetischen Rekonstruktion kombiniert die Anfangswahrscheinlichkeit, also A-priori-Wahrscheinlichkeit eines Baums P(tree) mit der Wahrscheinlichkeit der Daten (P|data), um eine A-posteriori-Wahrscheinlichkeitsverteilung auf Bäumen P(data|tree) zu erzeugen (Nascimento et al. 2017). Die A-posteriori-Wahrscheinlichkeit ist die Wahrscheinlichkeit, mit der Beobachtungen auf der Grundlage der Daten Gruppen zugewiesen werden. in unserem Fall wäre die A-Posteriori-Wahrscheinlichkeit eines phylogenetischen Baums die Wahrscheinlichkeit, dass der vorliegende Baum korrekt ist, wenn die Anfangswahrscheinlichkeit, die Daten und das Likelyhood-Modell gegeben sind.

Da die Zahl der möglichen Bäume in der Regel sehr groß ist, können wir ihre posterioren Wahrscheinlichkeiten in der Regel nicht analytisch berechnen. Wir können jedoch die Bäume finden, die nicht vernachlässigbare Posterior-Wahrscheinlichkeiten haben, und schätzen, wie hoch diese Wahrscheinlichkeiten sind, indem wir eine Computersoftware verwenden, die Stichproben von Bäumen aus einer Population simuliert, in der jeder mögliche Baum mit einer Häufigkeit vertreten ist, die seiner Posterior-Wahrscheinlichkeit entspricht (Huelsenbeck et al. 2001). Der verwendete Algorithmus bewegt sich von Baum zu Baum, wobei er mehr Zeit mit Bäumen verbringt, die höhere Wahrscheinlichkeiten haben, und macht regelmäßig eine Momentaufnahme des Baumes, bei dem er sich gerade befindet. Nachdem eine große Anzahl von Schnappschüssen gesammelt wurde, kann der Computer die posterioren Wahrscheinlichkeiten schätzen, indem er ermittelt, wie oft jeder mögliche Baum in der Schnappschusssammlung auftaucht. Der Reiz der Bayes’schen Phylogenie-Inferenz liegt darin, dass ihre Ergebnisse leicht zu interpretieren sind. Abb. 15 zeigt die Ergebnisse für die zuvor verwendeten 1.100-Nukleotid-β-Casein-Sequenzen. Abb. 15a zeigt die posterioren Wahrscheinlichkeiten der drei Bäume, die in den Schnappschüssen auftauchten. Diese summieren sich zu 1. Abb. 15b zeigt den Konsensbaum, der auf der Mehrheitsregel der Momentaufnahmen basiert. Jede Klade ist mit der Summe der posterioren Wahrscheinlichkeiten der Bäume, in denen sie vorkommt, gekennzeichnet.

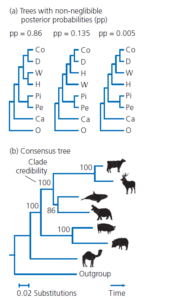
Abb. 15: Bayes’sche Phylogenie-Inferenz. Geschätzter Baum aus denselben Daten wie in Abb. 13, mit MrBayes (Ronquist & Huelsenbeck 2003).

Vergleich von Methoden der Phylogenie

 

Nachdem wir eine Vielzahl von Methoden zur Rekonstruktion der Evolutionsgeschichte aus Sequenzdaten kennengelernt haben, stellt sich natürlich die Frage, wie gut sie funktionieren. Forscher haben versucht, diese Frage zu beantworten, indem sie bekannte Evolutionsgeschichten erstellten und prüften, ob verschiedene Methoden der Phylogenieableitung die wahren Evolutionsbäume wiederherstellen können. Manchmal handelt es sich bei den bekannten Evolutionsgeschichten um Stämme von Organismen, wie z. B. Viren, die im Labor gezüchtet wurden (Hillis et al. 1992; Hillis et al. 1994; Sousa et al. 2008). Häufiger handelt es sich um Sequenzen, die durch Computersimulation entwickelt wurden (Guidon & Gascuel 2003; Hall 2005; Kolaczkowski & Thornton 2005). Solche Studien zeigen, dass unter optimalen Bedingungen alle von uns besprochenen Methoden – Parsimonie, Maximum Likelihood, Neighbour Joining und Bayes’sche Inferenz – das Verzweigungsmuster im wahren Baum mit einer Genauigkeit von nahezu 100 % wiederherstellen.

Alle Methoden haben ihre Stärken und Schwächen (Felsenstein 1978; Kolaczkowski & Thornton 2005). Aus diesem Grund verwenden Forscher oft eine Vielzahl von Methoden und überprüfen, ob die von ihnen erstellten Bäume miteinander übereinstimmen (Huelsenbeck & Hillis 1993; Hillis et al. 1994). Die Inferenz von Phylogenien ist ein aktives Forschungsgebiet, und es werden ständig neue Methoden entwickelt (Liu et al. 2009; Liu et al. 2011; Edwards 2009).

Im Zuge der Erörterung von Techniken zur Analyse von Sequenzdaten haben wir die β-Casein-Sequenzen einer gründlichen Prüfung unterzogen. Alle unsere Stammbäume weisen auf die gleiche Schlussfolgerung hin. Wale sind nicht nur mit den Paarhufern verwandt, sie sind Paarhufer. Und unsere Analysen unterstützen die Hypothese, dass Wale und Flusspferde Schwestertaxa sind. Die Wal-Hippo-Hypothese wurde durch die Analysen anderer Gene und weiteren Taxa zusätzlich unterstützt (Gatesy et al. 1999).

Aber die vorher vorgestellten morphologischen Untersuchungen bekräftigen eher die Hypothese, dass Wale zwar mit den Paarhufern verwandt sind, jedoch selbst nicht dazu gehören. Der offensichtliche Konflikt zwischen den Implikationen der molekularen und der morphologischen Daten veranlasste zu einer Suche nach anderen Datenquellen. Dies führte zu Entdeckungen sowohl in der Paläontologie als auch in der Molekularbiologie.

 

Auf dem Weg zu einer Lösung zur Phylogenie der Wale

 

Die neuen molekularen Daten, die die Phylogenie der Wale klären, wurden vor den Fossilienfunden gewonnen. Bei den molekularen Daten handelt es sich um das Vorhandensein oder Fehlen von DNA-Sequenzen, die sich gelegentlich an neuen Stellen in einem Genom einfügen. Die betreffenden genetischen Elemente werden als SINEs und LINEs bezeichnet, was für Short bzw. Long INterspersed Elements steht. Das Vorhandensein oder Fehlen einer bestimmten SINE oder LINE an einer homologen Stelle in den Genomen zweier verschiedener Arten kann als Merkmal bei der Ableitung der Phylogenie verwendet werden.

Die Vorteile der Verwendung dieser Daten bei der Stammesgeschichte ist, dass solche Transpositionsereignisse, bei denen sich ein parasitäres genetisches Element an einer neuen Stelle im Wirtsgenom einfügt, relativ selten sind. Daher ist es unwahrscheinlich, dass sich zwei homologe SINEs in zwei unabhängige Wirtslinien an genau der gleichen Stelle einfügen. Diese Art von Konvergenz ist zwar möglich, aber unwahrscheinlich. Auch die Umkehrung des ursprünglichen Zustands ist unwahrscheinlich, da der Verlust einer SINE oder LINE in der Regel nachgewiesen werden kann. Wenn SINEs und LINEs verloren gehen, ist es üblich, auch den damit verbundenen Verlust eines Teils des Wirtsgenoms zu beobachten. Daher können die Forscher in der Regel feststellen, ob ein bestimmtes parasitäres Gen fehlt oder verloren gegangen ist. Wenn Konvergenz und Umkehrung selten sind oder festgestellt werden können, dann ist Homoplasie unwahrscheinlich. SINEs und LINEs sollten außerordentlich zuverlässige Merkmale sein, die bei der Ableitung der Phylogenie verwendet werden können (Hillis 1999).

Was sagen SINEs und LINEs über die Evolution der Wale aus? Eine Arbeitsgruppe untersuchte 20 verschiedene SINEs und LINEs, die in den Genomen von Paarhufern vorkommen (Nikaido et al. 1999; Abb. 16).

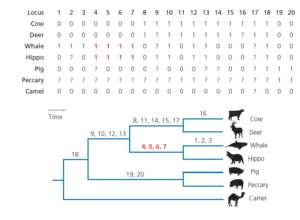
Abb. 16: Nahezu perfekte phylogenetische Merkmale? Diese Tabelle zeigt das Vorhandensein (1) oder Fehlen (0) einer SINE oder LINE an 20 Loci in den Genomen von sechs Paarhufern und einem Wal (Baird-Schnabelwal, Berardius bairdii). Fragezeichen (?) kennzeichnen Loci, die bei einigen Taxa fragwürdig sind. Taxa fragwürdig sind. Die Daten stammen von Nikaido et al. (1999). Der phylogenetische Baum wurde durch eine Parsimonie-Analyse dieser 20 Merkmale erstellt. Das Vorhandensein einer SINE oder LINE an den Loci 4-7 definiert eine Klade von Walen und Nilpferden.

Schaut man sich jedes dieser 20 genetischen Marker der Reihe nach an, wird man feststellen, dass das Vorhandensein oder Fehlen jedes SINE oder LINE als Synapomorphie fungiert, die genau eine Klade in der Phylogenie identifiziert. Anders ausgedrückt: In diesem Datensatz gibt es überhaupt keine Homoplasie und somit auch keinen Konflikt zwischen den Merkmalen, wenn sie auf den Baum abgebildet werden. Die Analyse ist bemerkenswert sauber und bestätigt nachdrücklich die Schlussfolgerungen aus den DNA-Sequenzstudien.

Nur wenig später nach dieser im Jahr 1999 durchgeführten Studie gaben zwei Forscherteams gleichzeitig Fossilfunde bekannt, die als “eines der wichtigsten Ereignisse im vergangenen Jahrhundert der Wirbeltierpaläontologie” bezeichnet wurden (de Muizon 2001). Die ältesten Fossilien stammten aus 48 Millionen Jahre alten Gesteinen und repräsentierten zwei Arten: den fuchsgroßen Ichthyolestes pinfoldi und den wolfsgroßen Pakicetus attocki (Thewissen et al. 2001). Bei beiden handelte es sich um langbeinige, langschwänzige Kreaturen, die eindeutig terrestrisch lebten. Beide Arten weisen die Synapomorphien an Schädel und Ohrknochen auf, die für Wale typisch sind, sowie den scheibenartigen Astragalus, der für die Paarhufer typisch ist (Abb. 17).

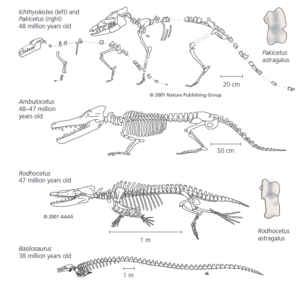
Abb. 17: Wale sind Paarhufer. Die hier abgebildeten Fossilien dokumentieren die Anatomie von Tieren mit abgeleiteten Schädelmerkmalen, die für Wale charakteristisch sind, und abgeleiteten Knöchelmerkmalen, die für Paarhufer charakteristisch sind. Die Fossilien dokumentieren auch einige der Veränderungen, die früh in der Evolution der Wale auftraten, als die Mitglieder dieses Stammbaums den Übergang vom Land zum Wasser vollzogen. Ichthyolestes und Pakicetus, sowie der Astragalus von Pakicetus nach Thewissen et al. (2001). Ambulocetus nach Thewissen et al. (1994). Rodhocetus nach Gingerich et al. (2001). Rodhocetus-Astragalus nach Uhen (2010). Basilosaurus nach Gingerich et al. (1990).

Die gleichen Merkmale finden sich auch bei zwei etwas jüngeren Arten, Artiocetus clavis und Rodhocetus kasrani, die auf 47 Millionen Jahre datiert wurden (Gingerich et al. 2001). Zusammengenommen bestätigen die neuen Fossilien, was die molekularen Daten uns schon lange sagen. Wale sind Paarhufer (Uhen 2010). Die Fossilien belegen nun, dass der Übergang zu einer aquatischen Lebensweise in einer Abstammungslinie von Paarhufern stattfand, aus der die heutigen Wale hervorgingen. Jüngste Analysen des Fossilnachweises haben auch eine ausgestorbene Gruppe semiaquatischer Paarhufer als Schwestergruppe der Flusspferde identifiziert (Boisserrie et al. 2005). Dieser Bericht stellt eine Verbindung zwischen den Vorfahren der heutigen Flusspferde und den Vorfahren der heutigen Wale und legt nahe, dass beide von demselben semiaquatischen Vorfahren abstammen (Orliac et al. 2010).

 

Literatur

 

Bajpai, S., and P. D. Gingerich. 1998. A new Eocene archaeocete (Mammalia, Cetacea) from India and the time of origin of whales. Proceedings of the National Academy of Science, USA 95: 15464–15468.

Baldauf, S. L. 2003. Phylogeny for the faint of heart: A tutorial. Trends in Genetics 19: 345–351.

Bayes, T. 1763. An essay towards solving a problem in the doctrine of chances. Philosophical Transactions of the Royal Society 53: 370–418.

Boisserie, J.-R., F. Lihoreau, and M. Brunet. 2005. The position of Hippopotamidae within Cetartiodactyla. Proceedings of the National Academy of Sciences, USA 102: 1537-1541.

Campbell, K. L., J. E. Roberts, et al. 2010. Substitutions in woolly mammoth hemoglobin confer biochemical properties adaptive for cold tolerance. Nature Genetics 42: 536–540.

Chevenet, F., C. Brun, et al. 2006. TreeDyn: Towards dynamic graphics and annotations for analyses of trees. BMC Bioinformatics 7: 439.

de Muizon, D. 2001.Walking with whales. Nature 413: 259–260.

Dereeper, A., V. Guignon, et al. 2008. Phylogeny.fr: Robust phylogenetic analysis for the non-specialist. Nucleic Acids Research 36: W465–W469.

Edwards, S. V. 2009. Is a new and general theory of molecular systematics emerging? Evolution 63: 1–19.

Felsenstein, J. 1978. Cases in which parsimony or compatibility methods will be positively misleading. Systematic Zoology 27: 401–410.

Felsenstein, J. 1981. Evolutionary trees from DNA sequences: A maximum likelihood approach. Journal of Molecular Evolution 17: 368–376.

Felsenstein, J. 1988. Phylogenies from molecular sequences: Inference and reliability. Annual Review of Genetics 22: 521–565.

Felsenstein, J. 2004. Inferring Phylogenies. Sunderland, MA: Sinauer.

Felsenstein, J. 2009. PHYLIP (Phylogeny Inference Package), Version 3.69. Distributed by the author. Department of Genome Sciences, University of Washington, Seattle. http://evolution.genetics.washington.edu/phylip/

Flower, W. H. 1883. On whales, past and present, and their probable origin. Nature 28: 199–202, 226–230.

Gatesy, J., M. Milinkovitch, et al. 1999. Stability of cladistic relationships between Cetacea and higher-level Artiodactyl taxa. Systematic Biology 48:6–20.

Gingerich, P. D. 2001. Research on the origin and early evolution of whales (Cetacea). http://www-personal.umich.edu/~gingeric/PDGwhales/Whales.htm

Gingerich, P. D., B. H. Smith, and E. L. Simons. 1990. Hind limbs of Eocene Basilosaurus: Evidence of feet in whales. Science 249: 154–157.

Gingerich, P. D., M. ul Haq, et al. 2001. Origin of whales from early artiodactyls: Hands and feet of Eocene Protocetidae from Pakistan. Science 293: 2239–2242.

Graur, D., and W.-H. Li. 2000. Fundamentals of Molecular Evolution. 2nd ed. Sunderland, MA: Sinauer.

Green, R. E., J. Krause, et al. 2010. A draft sequence of the Neandertal genome. Science 328: 710–722.

Guindon, S., J. F. Dufayard, et al. 2010. New algorithms and methods to estimate maximum-likelihood phylogenies: Assessing the performance of PhyML 3.0. Systematic Biology 59: 307–321.

Guindon, S., and O. Gascuel. 2003. A simple, fast, and accurate algorithm to estimate large phylogenies by maximum likelihood. Systematic Biology 52: 696–704.

Harrison, C. J., and J. A. Langdale. 2006. A step by step guide to phylogeny reconstruction. Plant Journal 45: 561–572.

Hall, B. G. 2005. Comparison of the accuracies of several phylogenetic methods using protein and DNA sequences. Molecular Biology and Evolution 22: 792–802

Hall, B. G. 2011. Phylogenetic Trees Made Easy: A How-To Manual. 4th ed. Sunderland, MA: Sinauer

Hillis, D. M. 1999. SINEs of the perfect character. Proceedings of the National Academy of Sciences, USA 96: 9979–9981.

Hillis, D. M., J. J. Bull, et al. 1992. Experimental phylogenetics: Generation of a known phylogeny. Science 255: 589–592.

Hillis, D. M., J. P. Huelsenbeck, and C. W. Cunningham. 1994. Application and accuracy of molecular phylogenies. Science 264: 671–677.

Huelsenbeck, J. P., and K. A. Crandall. 1997. Phylogeny estimation and hypothesis testing using maximum likelihood. Annual Review of Ecology and Systematics 28: 437–466.

Huelsenbeck, J. P., and D. M. Hillis. 1993. Success of phylogenetic methods in the four-taxon case. Systematic Biology 42: 247–264.

Huelsenbeck, J. P.; Ronquist, F. 2001. MRBAYES: Bayesian inference of phylogenetic trees. Bioinformatics. 17 (8): 754–755.

Huelsenbeck, J. P., F. Ronquist, et al. 2001. Bayesian inference of phylogeny and its impact on evolutionary biology, Supporting Online Material. Science 294: 2310–2314.

Kolaczkowski, B., and J. W. Thornton. 2004. Performance of maximum parsimony and likelihood phylogenetics when evolution is heterogeneous. Nature 431: 980–984.

Lari, M., E. Rizzi, et al. 2011. The complete mitochondrial genome of an 11,450-year-old Aurochsen (Bos primigenius) from Central Italy. BMC Evolutionary Biology 11: 32.

Li, S.; Pearl, D. K.; Doss, H. 2000. Phylogenetic Tree Construction Using Markov Chain Monte Carlo. Journal of the American Statistical Association. 95 (450): 493–508.

Liu, K., S. Raghavan, et al. 2009. Rapid and accurate large-scale coestimation of sequence alignments and phylogenetic trees. Science 324: 1561–1564.

Liu, K., T. J. Warnow, et al. 2011. SATé-II: Very fast and accurate simultaneous estimation of multiple sequence alignments and phylogenetic trees. Systematic Biology 61: 90–106.

Luckett, W. P., and N. Hong. 1998. Phylogenetic relationships between the orders Artiodactyla and Cetacea: A combined assessment of morphological and molecular evidence. Journal of Mammalian Evolution 5: 127–182.

Mau, B.; Newton, M. A.; Larget, B. 1999. Bayesian Phylogenetic Inference via Markov Chain Monte Carlo Methods. Biometrics. 55 (1): 1–12.

Nascimento, F. F.; Reis, M; Yang, Z. 2017. A biologist’s guide to Bayesian phylogenetic analysis. Nature Ecology & Evolution. 1 (10): 1446–1454.

Nikaido, M., A. P. Rooney, and N. Okada. 1999. Phylogenetic relationships among cetartiodactyls based on insertions of short and long interspersed elements: Hippopotamuses are the closest extant relatives of whales. Proceedings of the National Academy of Sciences, USA 96: 10261–10266.

Nummela, S., J. G. Thewissen, et al. 2007. Sound transmission in archaic and modern whales: Anatomical adaptations for underwater hearing. Anatomical Record: Advances in Integrative Anatomy and Evolutionary Biology 290: 716–733.

O’Leary, M. A., and J. H. Geisler. 1999. The position of Cetacea within Mammalia: Phylogenetic analysis of morphological data from extinct and extant taxa. Systematic Biology 48: 455–490.

Ogden, T. H., and M. S. Rosenberg. 2006. Multiple sequence alignment accuracy and phylogenetic inference. Systematic Biology 55: 314–328.

Orliac, M., J. R. Boisserie, et al. 2010. Early Miocene hippopotamids (Cetartiodactyla) constrain the phylogenetic and spatiotemporal settings of hippopotamid origin. Proceedings of the National Academy of Sciences, USA 107: 11871–11876.

Rannala, B.; Yang, Z. 1996. Probability distribution of molecular evolutionary trees: A new method of phylogenetic inference. Journal of Molecular Evolution. 43 (3): 304–311.

Ronquist, F., and J. P. Huelsenbeck. 2003. MRBAYES 3: Bayesian phylogenetic inference under mixed models. Bioinformatics 19: 1572–1574.

Saitou, N., and M. Nei. 1987. The neighbor-joining method—A new method for reconstructing phylogenetic trees. Molecular Biology and Evolution 4: 406–425.

Schaeffer, B. 1948. The origin of a mammalian ordinal character. Evolution 2: 164–175.

Sousa, A., L. Ze-Ze, et al. 2008. Exploring tree-building methods and distinct molecular data to recover a known asymmetric phage phylogeny. Molecular Phylogenetics and Evolution 48: 563–573.

Swofford, D. L., G. J. Olsen, et al. 1996. Phylogenetic inference. In Molecular Systematics, ed. D. M. Hillis, C. Moritz, et al. Sunderland, MA: Sinauer, 407–514.

Tamura, K., D. Peterson, et al. 2011. MEGA5: Molecular evolutionary genetics analysis using maximum likelihood, evolutionary distance, and maximum parsimony methods. Molecular Biology and Evolution 28: 2731-2739.

Thewissen, J. G. M., and S. T. Hussain. 1993. Origin of underwater hearing in whales. Nature 361: 444–445.

Thewissen, J. G. M., S. T. Hussain, and M. Arif. 1994. Fossil evidence for the origin of aquatic locomotion in archaeocete whales. Science 263: 210–212.

Thewissen, J. G. M., and S. I. Madar. 1999. Ankle morphology of the earliest cetaceans and its implications for the phylogenetic relations among ungulates. Systematic Biology 48: 21–30.

Thewissen, J. G. M., S. I. Madar, and S. T. Hussain. 1998. Whale ankles and evolutionary relationships. Nature 395: 452.

Thewissen, J. G. M., E. M. Williams, et al. 2001. Skeletons of terrestrial cetaceans and the relationship of whales to artiodactyls. Nature 413:277–281.

Uhen, M. D. 2007. Evolution of marine mammals: Back to the sea after 300 million years. Anatomical Record: Advances in Integrative Anatomy and Evolutionary Biology 290: 514–522.

Uhen, M. D. 2010. The origin(s) of whales. Annual Review of Earth and Planetary Sciences 38: 189–219.

Van Valen, L. M. 1966. Deltatheridia, a new order of mammals. Bulletin of the American Museum of Natural History 132: 1–126

Wang, L. S., J. Leebens-Mack, et al. 2011. The impact of multiple protein sequence alignment on phylogenetic estimation. IEEE–ACM Transactions on Computational Biology and Bioinformatics 8: 1108–1119.

Wong, K. M., M. A. Suchard, and J. P. Huelsenbeck. 2008. Alignment uncertainty and genomic analysis. Science 319: 473–476.

Yang, Z.; Rannala, B. (1 July 1997). “Bayesian phylogenetic inference using DNA sequences: a Markov Chain Monte Carlo Method”. Molecular Biology and Evolution. 14 (7): 717–724.