Unser Bild vom Universum und vom Sonnensystem hat sich in den letzten 500 Jahren dramatisch verändert. Damals dachten die meisten Menschen, dass die Erde eine Scheibe sei und sich im Zentrum des Universums befinde und dass die Sterne winzige Lichtpunkte auf der Himmelskuppel seien.
Doch heute wissen wir, dass die Erde ein Planet ist, welcher die Sonne umkreist (Abb. 1). Unsere Sonne ist einer von über 250 Milliarden Sternen unserer Heimatgalaxie, der Milchstraße. Von der Erde aus lassen sich mit aktueller Technik mehr als 50 Milliarden Galaxien beobachten. Seit 2016 geht die Forschung davon aus, dass sich im beobachtbaren Universum ca. eine Billion Galaxien befinden.
Text als pdf (deutsch)
English (pdf)
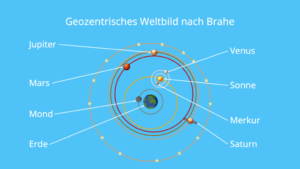
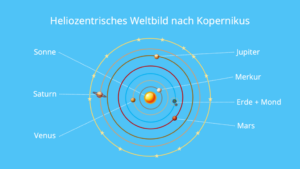
Abb. 1: geozentrisches und heliozentrisches Weltbild
Bevor wir aber die Ursprünge des Universums, der Materie und unseres Sonnensystems erkunden, ist es hilfreich einige physikalischer Gesetze kennenzulernen, die im ganzen Universum gelten. Wir lernen einige Prinzipien der Physik von Newton bis Einstein kennen.
Von Kopernikus bis Kepler
Alle Bewegungen, egal ob in Atomen oder in Galaxien, werden von wenigen physikalischen Gesetzen bestimmt. Die Erforschung des Weltalls begann dabei schon im 16. Jahrhundert. Im Jahr 1543 wies Kopernikus nach, dass die Sonne und nicht die Erde im Mittelpunkt unserer Welt steht und dass die Erde nur einer von mehreren Planeten ist, die um die Sonne kreisen (Siehe Abb. 1). Diese kopernikanische Wende beschleunigte die Entdeckung dieser Gesetze und Galilei leitete einige von ihnen aus seinen Experimenten ab. Im Jahr 1611 entdeckte Galilei mit einem der ersten Teleskope, dass die Sterne, die eine schier unendliche Anzahl haben, nicht auf einer großen Kuppel über unseren Köpfen verstreut sind. Er bestätigte auch, dass der Jupiter seine eigenen Monde hat und zeigte mit seinem Teleskop, dass der Erdmond mit Kratern übersät ist und keine perfekte Himmelskugel darstellt. Schließlich entdeckte er, dass die Venus wie der Mond ihre Phasen hat und zeigte, dass sich die Venus auf einer Bahn um die Sonne bewegt, die unserer eigenen Bahn entspricht. Vor allem aber bestätigte er Kopernikus’ Idee, dass die Erde nur einer von mehreren Planeten ist, der die Sonne umkreist.
Anfang des 17. Jahrhunderts hatte der Astronom Johannes Kepler die Gesetzmäßigkeiten, nach denen sich Planeten um die Sonne bewegen, hergeleitet. Sie sind bekannt als die Keplerschen Gesetze.
Das erste Keplersche Gesetz besagt, dass sich die Planeten auf elliptischen Bahnen bewegen. In einem gemeinsamen Brennpunkt steht die Sonne (Abb. 2).
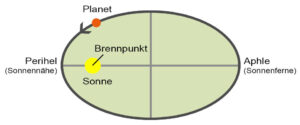
Abb. 2: erstes Kepler-Gesetz
Aus diesem Gesetz folgt, dass sich bei der Bewegung von Planeten um die Sonne der Abstand Planet-Sonne ständig ändert. So beträgt beispielsweise für die Erde der geringste Abstand von der Sonne 147,1 Mio. Kilometer (Perihel, Anfang Januar) und die größte Entfernung 152,1 Mio. Kilometer (Aphel, Anfang Juli). Die mittlere Entfernung der Erde von der Sonne hat einen Wert von 149,6 Mio. Kilometer. Diese Entfernung wird als Astronomische Einheit (Abkürzung: 1 AE) bezeichnet.
Das zweite keplersche Gesetz macht Aussagen über die Bewegung von Planeten längs ihrer Bahn. Es lautet: Die Verbindungslinie Sonne-Planet überstreicht in gleichen Zeiten gleich große Flächen (Abb. 3).
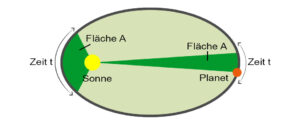
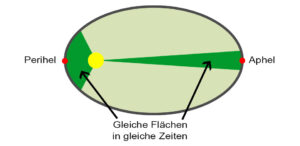
Abb. 3: 2. Kepler-Gesetz
Aus diesem Gesetz folgt, das sich die Planeten auf ihrer Bahn mit unterschiedlicher Geschwindigkeit bewegen. In Sonnennähe sind sie schneller als in Sonnenferne. Für die Erde betragen diese Geschwindigkeiten 29,3 km/s in Sonnenferne und 30,3 km/s in Sonnennähe.
Das dritte keplersche Gesetz beschreibt den Zusammenhang zwischen der Größe der Bahn und der Zeit für einen Umlauf um die Sonne. Es lautet: Die Quadrate der Umlaufzeiten zweier Planeten verhalten sich wie die dritten Potenzen der großen Halbachsen ihrer Bahnen (Abb. 4).
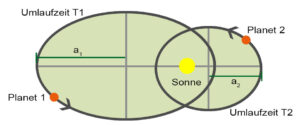
Abb. 4: 3. Kepler-Gesetz
Mithilfe dieses Gesetzes können aus den beobachtbaren Umlaufzeiten der Planeten um die Sonne die wahren Dimensionen des Planetensystems hergeleitet werden. Insbesondere folgt aus diesem Gesetz, dass die Bahngeschwindigkeit von Planeten mit wachsendem Abstand von der Sonne abnimmt. So bewegt sich z. B. Merkur als sonnennächster Planet schneller um die Sonne als die Erde. Die Erde bewegt sich ihrerseits schneller um die Sonne als die sonnenfernen Planeten Saturn oder Jupiter.
Die Keplerschen Gesetze gelten für die Planeten im Sonnensystem in guter Näherung. Die Abweichungen in den Positionen am Himmel sind meist kleiner als eine Winkelminute. Sie werden als Bahnstörungen bezeichnet und beruhen vor allem darauf, dass die Planeten nicht nur durch die Sonne angezogen werden, sondern sich auch untereinander anziehen.
Keplers drei Gesetze der Planetenbewegung stellen zum ersten Mal die menschliche Einsicht in die Natur des Universums auf eine sichere wissenschaftliche Grundlage. Nicht länger irrten die Planeten nach den Launen der Götter über den Himmel, stattdessen folgten sie mathematisch definierten Bahnen, die sich durch einfache Gesetze berechnen ließen. Sie sind bis heute von grundlegender Bedeutung in der Astronomie.
Newton
Trotz seiner Fortschritte wusste Kepler nicht, welche Kraft die Planeten in ihre Bahnen zwang. Diese Erklärung sollte erst 50 Jahre später gefunden werden.
Es war Isaak Newton der aus all den Teilbeschreibungen Kopernikus, Galileis und Keplers ein einfaches System von Gleichungen, das sowohl die Bewegungen als auch die Schwerkraft beschreibt, formulierte. Newton hat gezeigt, dass dieselben physikalischen Gesetze, die auf der Erde gültig sind, auch im Kosmos gelten. Daher können wir etwas über das Universum lernen, indem wir die physikalischen Gesetze hier auf der Erde studieren.
Newtons bekanntestes Werk ist die „Philosophiae Naturalis Principia Mathematica“ (dt. Die mathematischen Grundlagen der Naturphilosophie) von 1687. In diesem Werk vereint Newton die Forschungen Galileis zur Beschleunigung und Keplers zu den Planetenbewegungen zu einer einheitlichen Theorie der Gravitation und legte die Grundsteine der klassischen Mechanik, indem er die drei Grundgesetze der Bewegung formulierte.
Wir kennen Begriffe wie Geschwindigkeit, Beschleunigung, Kraft etc. Doch was bedeuten sie im physikalischen Sinne?
Die Geschwindigkeit ist eine Bewegung mit einer bestimmten Schnelligkeit in einer bestimmten Richtung, z. B. „100 km/h nordwärts“ (Abb. 5).

Abb. 5: Geschwindigkeit
Die Beschleunigung ist eine Geschwindigkeitsänderung (Abb. 6), also eine Änderung des Betrags oder der Richtung. Dabei ist auch eine Verringerung der Geschwindigkeit, z. B. durch Abbremsen, eine (negative) Beschleunigung.
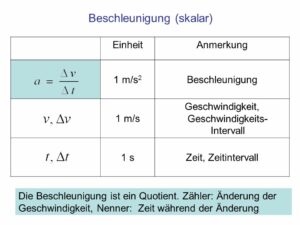
Abb. 6: Beschleunigung
Eine der wichtigsten Arten der Beschleunigung ist diejenige, die von der Gravitation (Schwerkraft) verursacht wird. Alle Objekte, unabhängig von ihrer Masse, erfahren dabei die gleiche Schwerebeschleunigung und mit „g“ abgekürzt. Allerdings wird die Schwerebeschleunigung durch den Luftwiderstand beeinflusst. Deswegen gleitet eine Feder leicht zu Boden, während ein Stein runterplumpst. In einem luftleeren Raum (Vakuum) fallen aber beide gleich schnell (Abb. 7). Auf der Erde bewirkt die Gravitation, dass fallende Objekte in jeder Sekunde 9,8m pro Sekunde schneller werden, also 9,8m pro Sekundenquadrat (g= 9,8m/s2).
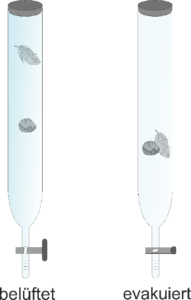
Abb. 7: freier Fall
Masse ist ein Maß für die Menge der Materie in einem Körper. Im Gegensatz dazu ist das Gewicht ein Maß für die Schwereanziehung, die auf einen Körper wirkt (Abb. 8). Die Masse eines Objekts ist immer gleich, egal, wo sich die Masse befindet. Das Gewicht verändert sich aber mit der Stärke der Schwerkraft oder anderen Kräften, die auf das Objekt wirken.
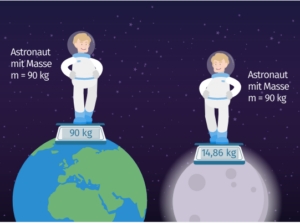
Abb. 8: Masse und Gewicht
Ein Objekt wird im freien Fall schwerelos, seine Masse bleibt dabei aber unverändert (Abb. 7). Der Fall eines Steines aus 20 m Höhe oder der Sprung einer Person von einem 10-m-Turm können als freier Fall betrachtet werden, da in diesen Fällen der Luftwiderstand vernachlässigt werden kann. Für einen am Fallschirm schwebenden Fallschirmspringer sind die Gesetze des freien Falls nicht anwendbar, weil in diesem Fall der Luftwiderstand nicht vernachlässigt werden kann.
Geschwindigkeit und Beschleunigung beschreiben, wie sich ein einzelnes Objekt bewegt, doch viele interessante Phänomene im Universum, beruhen auf der Wechselwirkung zwischen Objekten. Daher benötigen wir zwei weitere Begriffe, um diese Wechselwirkungen präzise beschreiben zu können: Impuls und Kraft.
Der Impuls ist Masse * Geschwindigkeit (p = mv). Der Impuls eines physikalischen Objekts ist umso größer, je schneller es sich bewegt und je massereicher es ist (Abb. 9).

Abb. 9: Impuls
Die einzige Möglichkeit, den Impuls eines Objektes zu verändern, besteht darin, eine Kraft darauf auszuüben, die ihn beschleunigt (Abb. 10). Folgerichtig ist Kraft = Masse * Beschleunigung (F= ma).
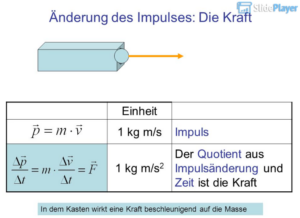
Abb. 10: Kraft
Irgendwelche Kräfte wirken immer, so beispielswiese die erwähnte Schwerkraft. Die resultierende Kraft, die auf ein Objekt wirkt, steht für die Kombination aller Kräfte (Abb. 11).
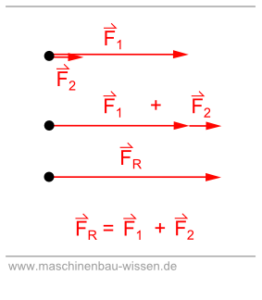
Abb. 11: Wirkung resultierender Kräfte
Wenn wir mit konstanter Geschwindigkeit fahren, gibt es keine resultierende Kraft, weil die vom Motor zum Antrieb der Räder erzeugte Kraft genau die Kräfte des Luftwiderstands und der Reibung ausgleicht. Eine Impulsänderung eines Objekts tritt nur auf, wenn die resultierende Kraft nicht gleich null ist, das Objekt also seine Geschwindigkeit ändert, sofern seine Masse konstant bleibt. Eine resultierende Kraft, die von null verschieden ist, bewirkt eine Beschleunigung des Objekts. Mithilfe derselben Vorstellungen können wir auch viele astronomische Vorgänge verstehen. So erfahren Planeten eine ständige Beschleunigung, während sie die Sonne umkreisen, weil sich die Bewegungsrichtung auf ihrer Umlaufbahn ständig ändert.
Ein Körper, der sich um seine Achse dreht oder entlang einer gekrümmten Bahn bewegt, wie das bei Planeten, aber z. B. auch bei einer Eiskunstläuferin, der Fall ist, hat einen Drehimpuls. Wirkt auf einen drehbar gelagerten Körper eine Kraft, ein sog. Drehmoment, so ändert sich sein Drehimpuls.
Aus diesen Erkenntnissen leitete Newton drei Bewegungsgesetze ab, die nicht nur unsere Bewegungen auf der Erde, sondern im gesamten Universum erklären.
- Newtonsche Gesetz: Ein Objekt bewegt sich mit konstanter Geschwindigkeit, wenn keine resultierende Kraft darauf wirkt.
- Newtonsche Gesetz: Kraft = Masse * Beschleunigung. In der Astronomie erklärt das zweite Newtonsche Gesetz, warum ein großer Planet wie der Jupiter einen größeren Einfluss auf Asteroiden und Kometen hat als ein kleiner Planet wie die Erde. Jupiter übt eine stärkere Gravitationskraft auf vorbeifliegende Objekte als die Erde aus, daher beschleunigt Jupiter die Asteroiden stärker.
- Newtonsche Gesetz: Zu jeder Kraft gibt es immer eine gleich große und entgegengesetzt gerichtete Kraft. Dieses Gesetz sagt beispielsweise, dass sich Objekte aufgrund der Gravitation immer gegenseitig anziehen. Unser Körper übt also eine große Anziehungskraft auf die Erde aus wie die Erde auf uns, nur dass diese Kraft in die entgegengesetzte Richtung weist. Natürlich bedeutet „die gleiche Kraft“ für uns eine wesentlich höhere Beschleunigung, weil unsere Masse im Vergleich zur Erde so gering ist. Deshalb fallen wir beim Sprung vom Stuhl auf die Erde und nicht die Erde auf uns.
Warum aber sollte eine jede Kraft eine gleichgroße und entgegengesetzt gerichtete Gegenkraft haben? Dies spiegelt wesentliche Aspekte der Natur wider, die als Erhaltungssätze bezeichnet werden. Körper haben eine Impulserhaltung, rotierende Körper eine Drehpulserhaltung.
Impulserhaltung bedeutet, dass sich der Impuls eines Objektes nicht verändern kann, es sei denn, es wird Impuls auf ein anderes oder von einem anderen Objekt übertragen. Wenn keine Kraft einwirkt, kann kein Impuls übertragen werden, daher behält ein Objekt Geschwindigkeit und Richtung bei.
Drehimpulserhaltung bedeutet, dass sich z. B. die Rotation um die Umlaufbahn eines Planeten oder die Eigenrotation nicht verändern können, es sei denn, er würde Drehimpuls auf ein anderes Objekt übertragen. Die Planeten unseres Sonnensystems tauschen untereinander oder mit anderen Objekten keine wesentlichen Drehimpulsbeträge aus, daher bleiben ihre Umlaufbahnen und Drehgeschwindigkeiten weitgehend stabil. Die Erde benötigt keinen Treibstoff oder irgendeine Art von Stoß, um weiter um die Sonne zu kreisen – sie wird die Bewegung fortsetzen, solange nichts des Weges kommt und ihr Drehimpuls abnimmt. Der Bahndrehimpuls der Erde ist das Produkt ihrer Geschwindigkeit und ihrer Entfernung zur Sonne. Die Bahngeschwindigkeit der Erde wird also größer, je näher sie sich an der Sonne befindet.
Auch die Energie bleibt immer erhalten – sie kann weder erzeugt noch zerstört werden. Alle Objekte haben jedwede Energie, die sie nun besitzen, durch den Austausch mit anderen Objekten bekommen. Energie tritt im Wesentlichen in drei Kategorien auf, als kinetische Energie (auch Bewegungsenergie genannt), Strahlungsenergie und potentielle Energie. Die potentielle Energie, bzw. gespeicherte Energie kann zu einem späteren Zeitpunkt in kinetische oder Strahlungsenergie umgewandelt werden.
Newton drückte die Gravitationskraft mathematisch in seinem allgemeinen Gravitationsgesetz aus (Abb. 12). Dabei zieht jede Masse jede andere Masse durch die Gravitationskraft an. Die Stärke der Gravitationskraft, die zwei Objekte aufeinander ausüben, ist dem Produkt ihrer Massen direkt proportional. Verdoppelt man die Masse eines Objektes, so verdoppelt man die Gravitationskraft zwischen beiden Objekten. Die Stärke der Gravitationskraft zwischen zwei Objekten fällt mit dem Quadrat des Abstands zwischen ihren Zentren ab. Verdoppelt man die Entfernung zwischen zwei Objekten, so verringert sich die Gravitationskraft um einen Faktor 4. Mathematisch wird dies in der Gleichung
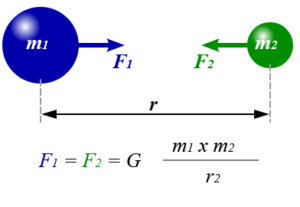
Abb. 12: Gravitationsgesetz
ausgedrückt. M1 und M2 sind die Massen der Objekte, r ist die Entfernung zwischen ihren Zentren und G steht für die Gravitationskonstante.
Die vorhin erwähnten Keplerschen Gesetze sind Folgerungen der Bewegungsgesetze und des allgemeinen Gravitationsgesetzes. Newton zeigte, dass jedes Objekt, das ein anderes umkreist, die beiden ersten Keplerschen Gesetze erfüllt. Er zeigte, dass geschlossene Umlaufbahnen auf Ellipsen (zu denen auch Kreise zählen) nicht die einzigen möglichen Bahnformen sind. Es gibt auch offene Bahnen in Form von Hyperbeln und Parabeln. So bewegen sich z. B. einige Kometen, die in das Innere eines Sonnensystems eintreten. Newton wies auch nach, dass zwei Himmelskörper eigentlich ihren gemeinsamen Schwerpunkt umkreisen. Mond und Erde ziehen ihre Bahnen um den gemeinsamen Schwerpunkt, aber da die Erde wesentlich massereicher ist als der Mond, liegt der gemeinsame Schwerpunkt etwa 1700 km unter der Erdoberfläche. Die newtonsche Fassung des dritten Keplergesetzes ermöglich es des Weiteren die Massen von umlaufenden Himmelskörpern aufgrund ihrer Umlaufperioden und Entfernungen zu berechnen.
Das Problem mit dem Merkurperihel
Mehr als zwei Jahrhunderte lang hatten die Gesetze von Isaac Newton jede erdenkliche Prüfung bestanden und schienen eine grundlegende Wahrheit des Universums darzustellen.
Was z. B. die Skeptiker schließlich von der Richtigkeit der Newtonschen Ideen überzeugte, war die von Edmund Halley berechnete Bahn eines besonders hellen Kometen und seine Vorhersage, dass er nach 76 Jahren wiederkehren würde. Als der Komet – der später als Halleyscher Komet bezeichnet wurde – Ende des Jahres 1758 wieder auftauchte, waren die Newtonschen Gesetze endgültig als korrekte Beschreibung der Welt und der sich in ihr bewegenden Körper anerkannt worden.
Aber gegen Ende des 19. Jahrhunderts erkannte eine immer größer werdende Zahl von Astronomen und Physikern, dass Newtons Theorien nicht immer die richtigen Antworten gaben.
Eine kleine Abweichung vom erwarteten Verhalten des Planeten Merkur war ein Hinweis darauf, dass das Gesetz der allgemeinen Gravitation nicht so allgemein gültig war, wie man es sich vorgestellt hatte.
Das Erste Keplersche Gesetz stellt fest, dass die Bahnen der Planeten Ellipsen einer ganz bestimmten Form und Größe sind. Beobachtungen zeigten aber, dass, obwohl Form und Größe bei jedem Umlauf gleichbleiben, die Bahn eines Planeten sich von Umlauf zu Umlauf ändert.
Der Punkt der größten Annäherung an die Sonne wird als Perihel bezeichnet. Wegen der gravitativen Anziehung der anderen Planeten ist der Ort des Perihels im Raum jedoch in Bewegung, er führt eine Präzession um die Sonne herum aus. Eine Präzession ist die Richtungsänderung der Achse eines rotierenden Körpers (Abb. 13).
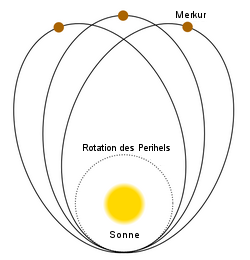
Abb. 13: Präzession des Planeten Merkur
Newton hat diese Präzession vorausgesagt. Genauere Studien zeigten jedoch, dass die Anziehung der anderen Planeten zwar für den größten Teil der beobachteten Präzession des Planeten Merkur verantwortlich gemacht werden kann, es aber einen kleinen, festen Anteil der Präzession gab, der nicht erklärt werden konnte – bis Albert Einstein die Bühne betrat.
Bevor wir uns mit Einstein und seinen Theorien befassen, müssen wir aber ein wenig zurück gehen, denn Einsteins Theorien kamen nicht aus dem Blauen heraus. Zunächst werden wir einige andere Wissenschaftler vorstellen, die durch ihre Forschungen über den Elektromagnetismus und die Lichtgeschwindigkeit den Weg für Einsteins Revolution bereiteten.
James Clerk Maxwell
Zu erwähnen ist hier James Clerk Maxwell. Seine bedeutendste Erkenntnis war, dass Elektrizität und Magnetismus eng miteinander verwandt sind. Beides sind Manifestationen der gleichen Sache, die er als elektromagnetisches Feld bezeichnete. Maxwells Theorie elektromagnetischer Felder konzentriert sich auf den Raum in der Nachbarschaft von elektrischen oder magnetischen Körpern.
Magnete haben einen Nord- und einen Südpol. Wenn wir zwei Magneten mit ihren Nordpolen (oder ihren Südpolen) zusammenbringen, tritt eine abstoßende Kraft auf. Wenn wir aber den Südpol eines Magneten mit dem Nordpol des anderen zusammenbringen, ziehen sich die Magnete an und bleiben aneinander haften. Was passiert, wenn wir Eisenfeilspäne auf ein Blatt Papier streuen und einen Magneten unter das Papier halten? Die Späne ordnen sich in einer Reihe gekrümmter Linien an, die man als magnetische Feldlinien bezeichnet und vom Nordpol zum Südpol laufen (Abb. 14).
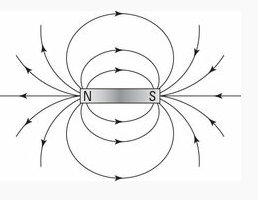
Abb. 14: Magnetfeldlinien
Diese Linien zeigen die elektromagnetische Kraft, die ein Körper erfährt, wenn er von einem Feld beeinflusst wird. Die Richtung der Linien zeigt die Richtung, in der die Kraft wirkt, und die Dichte der Linien verrät etwas über die Stärke der Kraft.
Es stellt sich heraus, dass elektrisch geladene Körper ebenfalls Felder erzeugen (Abb. 15). Stellen wir uns zwei Stahlkugeln vor, eine mit einer negativen elektrischen Ladung, die andere mit einer positiven. Bringen wir positiv geladene Kügelchen in die Nähe dieser beiden Kugeln, sehen wir, dass ein Feld entsteht, welches den magnetischen Feldlinien ähnlichsieht. Maxwell zeigte, dass sie sich nicht nur ähnlichsehen, sondern unter gewissen Umständen auch gleich sind. Eine geschickte mathematische Berechnung ergab, dass ein sich bewegender Magnet ein elektrisches Feld erzeugt und dass eine sich bewegende elektrische Ladung ein magnetisches Feld erzeugt.
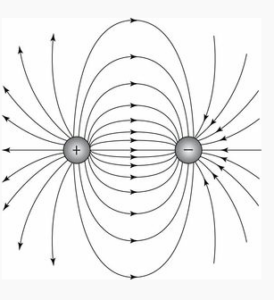
Abb. 15: elektrische Feldlinien
Das Bemerkenswerteste an Maxwells Gleichungen ist vielleicht deren Vorhersage, dass elektrische und magnetische Kräfte sich durch wellenartige Schwingungen mit einer festen Geschwindigkeit ausbreiten.
Maxwells Berechnungen zeigten, dass die Geschwindigkeit der elektromagnetischen Wellen bei 288.000 Kilometern pro Sekunde liegt, was fast genau mit der Lichtgeschwindigkeit übereinstimmt, die von dem französischen Wissenschaftler Hippolyte Fizeau 1849 mit Hilfe eines rotierenden Spiegels mit 313.000 Kilometern pro Sekunde gemessen worden war. Maxwell erkannte die Bedeutung dieses Zusammentreffens und kam zu der Schlussfolgerung, dass Licht (einschließlich anderer Strahlungen) eine Form der elektromagnetischen Strahlung ist (Abb. 16). Maxwells theoretische Überlegungen wurden später durch den deutschen Physiker Heinrich Hertz bestätigt, als er Radiowellen erzeugte, die eine andere Form elektromagnetischer Strahlung darstellen.
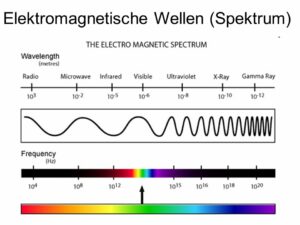
Abb. 16: elektromagnetische Wellen
Seine neuen Einsichten in den Elektromagnetismus stellten Maxwell vor ein weiteres Problem: Welches war der Träger all dieser Wellen? Seine Idee war, dass es eine Substanz gibt, die er „Lichtäther“ nannte, die den Raum erfüllt, alles durchdringt und in dem sich die elektromagnetischen Wellen ausbreiten wie der Schall in der Luft. Dieser Gedanke war schon seit der Zeit des Aristoteles verbreitet – das Problem war nur, dass es nie gelungen war, die Existenz eines solchen Äthers zu beweisen.
Die Abschaffung des Äthers
Maxwells Vorstellung, dass eine geheimnisvolle Substanz namens Äther für die Fortpflanzung elektromagnetischer Wellen im Raum nötig war, stellte zweifellos ein Problem für die Wissenschaftler dar. Dann dachten sich zwei in den USA lebende Wissenschaftler, Albert Abraham Michelson und Edward Williams Morley, ein Experiment aus, mit dem sie hofften, die Bewegung des Äthers – wenn er denn existierte – an der Erdoberfläche zu messen.
Die Experimente beruhten auf dem Gedanken, dass die um die Sonne kreisende Erde sich relativ zum Äther bewegt und deshalb eine Art von „Ätherwind“ nachweisbar sein sollte. Dieser Wind, dachten die Wissenschaftler, sollte kleine Änderungen in der Lichtgeschwindigkeit hervorrufen, die mittels Laborinstrumenten messbar sein sollten. Das Problem lag darin, dass der Unterschied in der Lichtgeschwindigkeit sehr klein sein würde.
Das Duo baute ein Experiment auf, in dem ein Lichtstrahl in zwei Einzelstrahlen aufgespalten wird, die sich im rechten Winkel zueinander ausbreiten (Abb. 17).
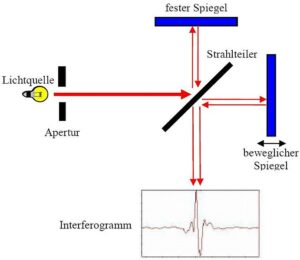
Abb. 17: Experiment von Michaelson und Morley
Zunächst schickten Michelson und Morley einen Lichtstrahl durch einen halbdurchlässigen Spiegel, der so beschaffen war, dass er die Hälfte des auf ihn fallenden Lichts reflektierte und die andere Hälfte durchließ. Durch die Beschaffenheit und den Winkel des Spiegels bewegte sich die Hälfte des Lichts geradeaus weiter, während die andere Hälfte im rechten Winkel abgelenkt wurde. Jeder der Lichtstrahlen wurde durch andere Spiegel reflektiert und kam schließlich bei einem Lichtdetektor, einer Mattscheibe, an. Im Lichtdetektor erzeugen die beiden Lichtstrahlen ein Interferenzmuster, eine Reihe von hellen und dunklen Streifen, die entstehen, wenn die beiden Lichtwellen wieder zusammengeführt werden. Dieser Versuchsaufbau wurde auf einem großen Marmorblock aufgebaut, der auf einem Quecksilberbecken schwamm, um alle Schwingungen zu unterdrücken, die den gesuchten Effekt vortäuschen könnten.
Michelson und Morley hofften, dass das von den beiden Lichtstrahlen hervorgerufene Interferenzmuster zeigen würde, dass die beiden Strahlen ihre zurückgelegten Wege mit wenig unterschiedlicher Geschwindigkeit zurücklegen würden. Aber ihre Versuche zeigten keinerlei Unterschied bei den verschiedenen Orientierungen oder zu verschiedenen Zeiten des Tages oder Jahres – ein klarer Hinweis darauf, dass die Vorstellung eines Äthers falsch war. Tatsächlich wurde das Experiment von vielen Wissenschaftlern seit den Versuchen von Michelson und Morley oft wiederholt, und das Ergebnis war immer das gleiche. Die Lichtgeschwindigkeit, meist abgekürzt mit dem Buchstaben c, ist also unabhängig vom Bezugssystem und beträgt im leeren Raum immer ca. 300.000 Meter pro Sekunde.
Ein paar Jahre mussten vergehen, bis die wirklichen Konsequenzen aus diesen Versuchen offenkundig wurden. Michelsons und Morleys Experiment legte nahe, dass es eine universelle konstante Lichtgeschwindigkeit gab, und dies brachte Einstein auf die Fährte zu seiner berühmtesten Gleichung, die die subtile Wechselwirkung zwischen Masse und Energie beschreibt, die im frühen Universum von großer Wichtigkeit ist.
Spezielle Relativitätstheorie
Albert Einstein nahm die Konstanz der Lichtgeschwindigkeit zum Anlass, die Existenz einer absoluten und allgemein gültigen Zeit in Frage zu stellen.
Wenn die Einsteinschen Relativitätstheorien auch gerne scherzhaft (und falsch) zu „alles ist relativ“ verallgemeinert werden: Einsteins Ausgangsfrage nach Relativität und Absolutheit ist sehr viel eingeschränkter. Sie beschäftigt sich nur mit einer ganz speziellen Klasse von Situationen und Beobachtern.
Stellen wir uns vor, dass wir uns in einem Eisenbahnzug befinden, der sich mit konstanter Geschwindigkeit von 100 km/h auf einem geraden Bahngleis bewegt. Während wir auf unserem Platz sitzen, geht ein Schaffner von vorn nach hinten durch den Zug, und zwar mit einer konstanten Geschwindigkeit von fünf Kilometern pro Stunde.
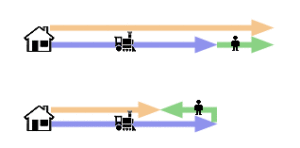
Abb. 18: Galileische Relativität
Aus unserer Sicht – oder in unserem Bezugssystem, wie die Physiker sagen – entfernt sich der Schaffner mit fünf Kilometern pro Stunde von uns. Um mit ihm Schritt zu halten, müssten wir ihm auch mit fünf Kilometern pro Stunde nachlaufen.
Aber für einen Freund auf dem Bahnsteig außerhalb des Zuges ist es viel schwieriger, mit dem Schaffner Schritt zu halten. Er muss sich mit einer anderen Geschwindigkeit bewegen – 100 Kilometer pro Stunde minus 5 Kilometer pro Stunde, oder 95 Kilometer pro Stunde – um mit dem Schaffner Schritt zu halten.
Wie groß ist also die Geschwindigkeit des Schaffners? Beträgt sie 5 Kilometer pro Stunde oder 95? Nun, das hängt von unserem Bezugssystem ab.
Anders ausgedrückt, es gibt für uns im Zug keine Möglichkeit festzustellen, ob sich der Schaffner mit 5 oder mit 95 Kilometern pro Stunde bewegt. Es gibt keine Methode, um zwischen der Ruhe und der gleichförmigen Bewegung zu unterscheiden. Wissenschaftler bezeichnen diese Erfahrung als Galileische Relativität.
Einstein erkannte, dass die Galileische Relativität auf eine Schwierigkeit stößt, wenn man elektromagnetische Erscheinungen (wie das Licht) betrachtet.
Bei seinem Versuch, die Galileische Relativität mit den Maxwellschen Gesetzen des Elektromagnetismus in Einklang zu bringen, arbeitete Einstein auf der Grundlage zweier Postulate:
- Die physikalischen Gesetze sind in allen nichtbeschleunigten Bezugssystemen die gleichen.
- Die Lichtgeschwindigkeit ist in allen nichtbeschleunigten Bezugssystemen die gleiche.
Um ein Gefühl dafür zu bekommen, wie die absolute Größe der Lichtgeschwindigkeit eine Verlangsamung der Zeit verursacht (Dilatation), stellen wir uns vor, dass wir uns in einem in Bewegung befindlichen Zug befinden – wieder einmal (Abb. 19)! Wir lassen einen Laserstrahl zwischen zwei Spiegeln hin- und herlaufen; der eine soll sich am Boden, der andere an der Decke des Wagens befinden.
Stellen wir uns vor, dass wir das Zeitintervall messen können, das das Licht benötigt, um vom Boden zur Decke und wieder zurück zu gelangen.
Nun stellen wir uns vor, dass ein auf dem Bahnsteig stehender Freund auch beobachten kann, wie das Licht hin- und herläuft. Er sieht es diagonal nach oben und dann wieder diagonal nach unten laufen. Von seinem Blickwinkel aus legt das Licht eine weitere Strecke zurück als von unserem eigenen.
Wenn die Gesetze der Physik – und insbesondere die Maxwellschen Gleichungen – in allen gleichförmig bewegten Bezugssystemen die gleichen sind, sollte die vom Zug aus beobachtete Lichtgeschwindigkeit die gleiche sein wie die vom Bahnsteig aus beobachtete.
Das Ende vom Lied ist folgendes: Wenn unser Freund auf dem Bahnsteig auf seiner Armbanduhr die Zeit misst, die für das Hin-und-Herlaufen des Lichtes benötigt wird, wird er feststellen, dass sie länger als eine Sekunde ist. Von seinem Blickwinkel aus betrachtet, vergeht im Zug die Zeit langsamer als für ihn auf dem Bahnsteig.
Die Lichtgeschwindigkeit ist für alle sich konstant bewegenden Beobachter die gleiche. Wie ist das möglich? Einsteins Antwort war, dass, obwohl die Lichtgeschwindigkeit konstant ist, die Zeit nicht gleichförmig verstreicht. Einsteins Spezielle Relativitätstheorie besagte, dass die Zeit für einen Beobachter in Bewegung gedehnt wird und dass der Raum sich für ihn zusammenzieht.
Im Juni 1905 veröffentlichte Einstein die Ergebnisse seiner Lösung in der Zeitschrift Annalen der Physik unter dem Titel „Über die Elektrodynamik bewegter Körper“.
Die Ergebnisse von Einsteins Berechnungen zeigten in der Tat, dass sie das in den Michelson-Morley-Experimenten aufgeworfene Problem lösten.
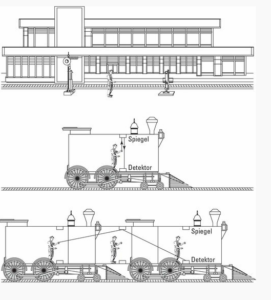
Abb. 19: (Oben) Sie sehen, wie der Lichtstrahl nach oben läuft, reflektiert wird und wieder nach unten läuft. (Unten) Ihr Freund sieht den Lichtstrahl entlang einer Diagonale nach oben laufen, und nach der Reflexion entlang einer anderen Diagonale nach unten laufen.
Diese Beobachtung ist eine der wichtigsten in der Speziellen Relativitätstheorie: In einem bewegten Bezugssystem vergeht die Zeit langsamer. Weil die Lichtgeschwindigkeit, die ja eine Strecke ist, die durch eine Zeit dividiert ist, konstant bleiben muss, konnte Einstein auch zeigen, dass in einem bewegten Bezugssystem sich der Raum zusammenzieht.
Plötzlich waren also Raum und Zeit nicht mehr die feste Bühne, auf der sich die Geschehnisse des Universums abspielten, wie es einst von Newton und anderen angenommen worden war. Diese Veränderlichkeit in Zeit und Raum mag uns seltsam erscheinen und so gar nicht zu den Erfahrungen des täglichen Lebens passen. Das liegt aber daran, dass wir uns niemals nahe der Lichtgeschwindigkeit bewegen. Aber wissenschaftliche Experimente haben immer wieder gezeigt, dass diese Änderung von Raum und Zeit wirklich auftritt.
Kurz nachdem Einstein seine Spezielle Relativitätstheorie im Juni 1905 veröffentlicht hatte, gab er eine weitere kurze Arbeit mit dem Titel „Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?“ zum Druck. In dieser Arbeit benutzte er die Prinzipien der Speziellen Relativitätstheorie, um zu zeigen, dass die Masse eines Atoms abnimmt, wenn es Licht oder eine andere elektromagnetische Strahlung aussendet, beispielsweise ein Laser oder eine radioaktive Quelle, die Röntgenstrahlen abgibt. Kurz gesagt, zeigte Einsteins Arbeit, dass die Masse eines Körpers ein Maß dafür ist, wie viel Energie in ihm steckt. Das heißt nichts anderes, als dass Materie und Energie austauschbar sind! Und was bedeutet das? E= mc2
Energie ist eine Form von Masse, und Masse ist eine Form von Energie. Weil der Faktor zwischen ihnen so eine große Zahl ist (das Quadrat der Lichtgeschwindigkeit), hat selbst das kleinste Stück Materie das Potenzial, eine enorme Energiemenge freizusetzen.
Die Masse eines Objekts nimmt zu, wenn seine Geschwindigkeit zunimmt. Wenn sich die Geschwindigkeit eines Objekts immer mehr der Lichtgeschwindigkeit nähert, wächst seine Masse immer mehr an, bis zu dem Punkt, bei dem es nicht mehr möglich ist, es weiter zu beschleunigen. Das ist auch der Grund, warum sich kein massereiches Objekt schneller als das Licht fortbewegen kann.
Allgemeine Relativitätstheorie
Einstein kannte die Bedeutung seiner Arbeit zur Speziellen Relativitätstheorie, aber er erkannte von Anfang an, dass seine Theorie auf eine bestimmte Art von Bewegung beschränkt war – eine Bewegung ohne Beschleunigung. Ein Jahrzehnt später, im Jahr 1916 entwickelte er schließlich die allgemeine Relativitätstheorie. Diese beschreibt die Wechselwirkung zwischen Materie einerseits sowie Raum und Zeit andererseits. Sie deutet Gravitation als geometrische Eigenschaft der gekrümmten vierdimensionalen Raumzeit. Um dies nachzuvollziehen, lassen wir uns auf ein Gedankenexperiment ein, den Einstein selbst durchführte.
Was passiert eigentlich in einem Fahrstuhl, wenn man die Kabel durchschnitte und alles – der Fahrstuhl mitsamt der Insassen – frei nach unten fiele (Abb. 20)?
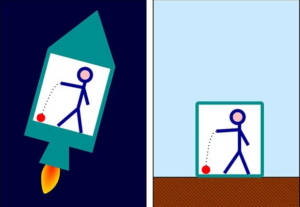
Abb. 20: Was passiert eigentlich in einem Fahrstuhl, wenn man die Kabel durchschnitte und alles – der Fahrstuhl mitsamt der Insassen – frei nach unten fiele?
Die fallenden Personen im Fahrstuhl könnten nicht erkennen, ob sie von der Schwerkraft heruntergezogen oder auf irgendeine andere Art und Weise mit der gleichen Rate beschleunigt werden. Einsteins Idee: Kein Physiker könnte durch ein noch so ausgeklügeltes Experiment entscheiden, ob er sich in einem Schwerefeld eines Körpers befindet oder in einem beschleunigten Bezugsrahmen, eben dem Aufzug.
Einstein folgerte, dass Beschleunigung und Schwerkraft austauschbar sind. Dieses „Äquivalenzprinzip“ wurde der Dreh- und Angelpunkt der allgemeinen Relativitätstheorie.
Einstein erkannte, dass die Tatsache, dass Schwerkraft und Beschleunigung austauschbar sind, eine große Bedeutung für das Licht hat.
Um dies zu verstehen, stellen wir uns vor, dass wir in einem Raumschiff sitzen, das beschleunigt durchs All fliegt (Abb. 21). Auf der Seite des Raumschiffs befindet sich ein kleines Loch, durch den ein Lichtstrahl eindringt und auf der gegenüberliegenden Kabinenwand einen Lichtfleck hervorruft.
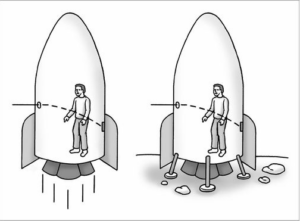
Abb. 21: In einem beschleunigten Raumschiff scheint für den Wissenschaftler ein Lichtstrahl gekrümmt zu sein.
Da das Raumschiff beschleunigt wird, stellt man fest, dass der Lichtfleck tiefer auf der Kabinenwand auftrifft, als wenn das Schiff stillstehen würde – so, als ob das Licht in einem Bogen zum Boden hin gekrümmt würde. Das mag noch alles recht einfach zu verstehen sein. Aber wir erinnern uns, dass Schwerkraft und Beschleunigung die gleiche Wirkung haben. Deshalb sollte die Schwerkraft den gleichen Einfluss auf den in das Raumschiff dringenden Lichtstrahl haben – er sollte sich ein wenig krümmen.
In der Allgemeinen Relativitätstheorie kann gezeigt werden, dass es nicht die Schwerkraft ist, die die Krümmung eines Lichtstrahls hervorruft. Stattdessen ist die Raumzeit – eine mathematische Konstruktion, die Raum und Zeit vereint und in der der Raum üblicherweise dreidimensional ist und die Zeit die Rolle einer vierten Dimension annimmt – selbst gekrümmt, und das Licht nimmt einfach den kürzesten Weg von der Quelle bis zu seinem Ziel.
Die vielleicht beste Art und Weise, sich die Raumzeit vorzustellen, ist, sich eine horizontal aufgespannte Gummihaut vorzustellen (Abb. 22).
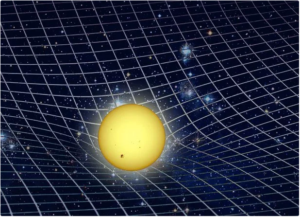
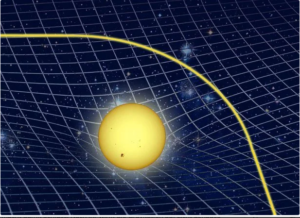
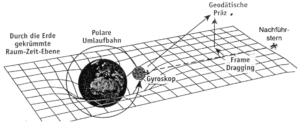
Abb. 22: Die Raumzeit, dargestellt in zwei Dimensionen. Die Masse krümmt die Raumzeit. Das Licht nimmt einfach den kürzesten Weg von der Quelle bis zu seinem Ziel
Nun stellen wir uns vor, dass wir eine Kanonenkugel in die Mitte der Gummifläche legen. Was geschieht jetzt? Die Kanonenkugel drückt die Gummifläche ein und verursacht eine Kuhle. Wenn wir nun eine Murmel über die Gummifläche rollen lassen, rollt sie in Richtung der Kanonenkugel. Wenn wir versuchen, die Murmel an der Kanonenkugel vorbeizurollen, wird sie eine gekrümmte Bahn zurücklegen.
Einsteins Allgemeine Relativitätstheorie zeigt, dass das, was wir als Schwerkraft empfinden – den Fall eines Apfels auf die Erde, die Kraft, die den Mond in seiner Bahn um die Erde hält und die Planeten um die Sonne – gar keine Kraft im wirklichen Sinne ist. Die Masse, die Raumzeit krümmt, lässt uns glauben, dass eine Kraft am Wirken ist.
Die Berechnung der Krümmung der Raumzeit ist eine Sache, der Beweis ihrer Realität eine andere. Selbst auf großen Skalen ist die Krümmung der Raumzeit ungeheuer klein. Einstein selbst erkannte das Problem, als er sagte, dass die Krümmung „extrem klein sei für die Schwerkraftfelder, mit denen wir in der Praxis zu tun haben“.
Um die Theorie der Krümmung der Raumzeit zu prüfen, müssen wir Licht untersuchen, das nahe an einem massereichen Himmelskörper, wie unserer Sonne, vorbeiläuft, denn dann kann man feststellen, ob die Schwerkraft des Körpers einen Lichtstrahl krümmt. Normalerweise ist die Sonne so hell, dass anderes Licht in ihrer Lichtfülle ertrinkt. Glücklicherweise liefert uns die Natur hin und wieder einen ausgezeichneten Sonnenschirm – eine totale Sonnenfinsternis (Abb. 23).

Abb. 23: Sonnenfinsternis
Hierfür schauen wir uns Sterne in der Nähe des Sonnenrandes an. Wenn Einstein recht hat, sollte der Ort eines Sterns in der Nähe des Sonnenrandes leicht verschoben werden, da das Licht, das vom Stern zu uns gelangt, durch die Schwerkraftanziehung gekrümmt wird.
Einstein berechnete, dass Sternlicht, das genau am Sonnenrand vorbeiläuft, um den winzigen Bruchteil eines Grades gekrümmt wird, der etwa der Größe eines Centstücks in einer Entfernung von 3 Kilometern entspricht (Abb. 24).
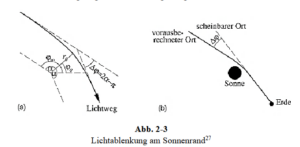
Abb. 24: Lichtablenkung am Sonnenrand
Wenn man den Ort des Sterns am Tag der Sonnenfinsternis mit einem in einem Sternatlas verzeichneten Ort vergleicht, kann man die Krümmung des Sternenlichts nachweisen.
Während der totalen Sonnenfinsternis vom 29. Mai 1919 besuchte der Astronom Arthur Eddington die Insel Principe an der afrikanischen Westküste und machte eine Aufnahme der Sterne in dem Sternhaufen der Hyaden, die sich zu dieser Zeit nahe dem Sonnenrand befanden. Obwohl Wolken eine Beobachtung fast unmöglich machten, klarte es doch genügend auf, um eine fotografische Aufnahme zu erhalten (Abb. 23). Eddington konnte Sterne erkennen und fand, dass die Verschiebung der Sterne den Einstein’schen Berechnungen entsprach.
Kommen wir zurück zum Merkurperiphel.
Dass sich die Merkurbahn ständig verändert, brachte die Astronomen in Erklärungsnot. Als Lösungsvorschläge kursierten Staub in der Nähe der Sonne, ein hypothetischer Planet noch innerhalb der Merkurbahn oder die Abplattung der Sonne. Doch keiner dieser Effekte konnte erklären, warum sich die Merkurbahn pro Jahrhundert um 43 Bogensekunden oder gerade mal gut 10.000 Kilometer verschiebt – dies gelang erst, als sich Albert Einstein des Problems annahm. Mit der allgemeinen Relativitätstheorie konnte die Abweichung der Merkurbahn, also diese 43 Bogensekunden, genau berechnet werden. Für Albert Einstein war die Merkurbahn ein ganz wichtiges Erfolgserlebnis bei der Entwicklung seiner Theorie.
In unserem Alltag fallen die Unterschiede zwischen dem Newtonschen und dem Einsteinschen Regelwerk zumeist nicht auf. Erst wenn es um große Massen und äußerste Präzision geht, sind auch die relativistischen Effekte zu berücksichtigen.
Als die Wissenschaftler das Universum immer gründlicher mit großen Teleskopen erforschten, entdeckten sie, dass das Licht entfernter Sterne auch ein sehr wichtiges Werkzeug darstellt, um die Expansion des Universums zu studieren. In der Tat – obwohl das Universum riesengroß ist, dehnt es sich immer weiter aus. Die Expansion des Universums erzählt uns viel über seinen Ursprung und seine Zukunft – und damit beschäftigen wir uns im nächsten Beitrag.
Literatur
Bennett, J. Donhaue, M., Schneider, N., Voit, M. (2020): Astronomie die kosmische Perspektive. Pearson Verlag, 9. Auflage
Maran, S. M. (2008): Astronomie für Dummies. Wiley VCH Verlag, 3. Auflage
Oschmann, W. (2016): Evolution der Erde. Utb
Pincock, S., Frary, M. (2009): Ursprung des Universums für Dummies. Wiley VCH Verlag, 1. Auflage
Lesch, H., Gaßner, J. M. (2020): Urknall, Weltall und das Leben. Verlag Komplett-Media, 4. Auflage